题目内容
已知一组数据x1,x2,…,xn的方差为s2,那么另一组新数据x1+a,x2+a,…,xn+a(a≠0)的方差是
s2 .
考点: 方差.
分析: 根据方差公式进行计算,方差是用来衡量一组数据波动大小的量,每个数都加上a所以波动不会变,方差不变.
解答: 解:根据题意得:
原数据的平均数为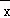 ,新数据的每一个数都加上了a,则平均数变为
,新数据的每一个数都加上了a,则平均数变为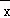 +a,
+a,
设原来的方差S2=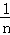 [(x1﹣
[(x1﹣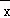 )2+(x2﹣
)2+(x2﹣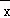 )2+…+(xn﹣
)2+…+(xn﹣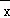 )2],
)2],
现在的方差S2=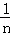 [(x1+a﹣
[(x1+a﹣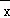 ﹣a)2+(x2+a﹣
﹣a)2+(x2+a﹣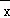 ﹣a)2+…(xn+a﹣
﹣a)2+…(xn+a﹣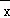 ﹣a)2]=
﹣a)2]=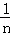 [(x1﹣
[(x1﹣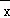 )2+(x2﹣
)2+(x2﹣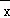 )2+…+(xn﹣
)2+…+(xn﹣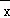 )2],
)2],
原来的方差与现在的方差一样,
则另一组新数据x1+a,x2+a,…,xn+a(a≠0)的方差是s2;
故答案为:s2.
点评: 此题考查了方差,一般地设n个数据,x1,x2,…xn的平均数为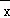 ,则方差S2=
,则方差S2=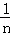 [(x1﹣
[(x1﹣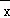 )2+(x2﹣
)2+(x2﹣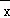 )2+…+(xn﹣
)2+…+(xn﹣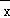 )2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
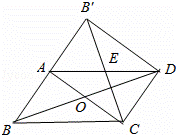
 中,自变量x的取值范围是
中,自变量x的取值范围是 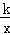 的一支在第一象限交梯形对角线OC于点D,交边BC于点E.
的一支在第一象限交梯形对角线OC于点D,交边BC于点E.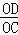 =
=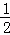 ,S△OAC=2,求双曲线的解析式.
,S△OAC=2,求双曲线的解析式.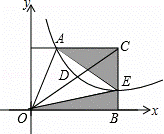
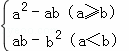 ,例如:4*2,因为4>2,所以4*2=42﹣4×2=8.若x1、x2是一元二次方程x2﹣8x+12=0的两个根,那么x1*x2=.
,例如:4*2,因为4>2,所以4*2=42﹣4×2=8.若x1、x2是一元二次方程x2﹣8x+12=0的两个根,那么x1*x2=.