ΧβΡΩΡΎ»ί
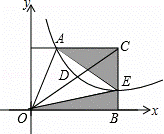
»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§Χί–ΈAOBCΒΡ±ΏOB‘Ύx÷αΒΡ’ΐΑκ÷α…œΘ§ACΓΈOBΘ§BCΓΆOBΘ§ΙΐΒψAΒΡΥΪ«ζœΏy=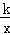 ΒΡ“Μ÷ß‘ΎΒΎ“ΜœσœόΫΜΧί–ΈΕ‘Ϋ«œΏOC”ΎΒψDΘ§ΫΜ±ΏBC”ΎΒψEΘ°
ΒΡ“Μ÷ß‘ΎΒΎ“ΜœσœόΫΜΧί–ΈΕ‘Ϋ«œΏOC”ΎΒψDΘ§ΫΜ±ΏBC”ΎΒψEΘ°
Θ®1Θ©ΧνΩ’ΘΚΥΪ«ζœΏΒΡΝμ“Μ÷ß‘ΎΒΎ»ΐœσœόΘ§kΒΡ»Γ÷ΒΖΕΈß «kΘΨ0ΘΜ
Θ®2Θ©»τΒψCΒΡΉχ±ξΈΣΘ®1Θ§1Θ©Θ§«κ”ΟΚ§”–kΒΡ ΫΉ”±μ Ψ“θ”Α≤ΩΖ÷ΒΡΟφΜΐSΘ°≤ΔΜΊ¥πΘΚΒ±ΒψE‘Ύ ≤Ο¥ΈΜ÷Ο ±Θ§“θ”Α≤ΩΖ÷ΟφΜΐSΉν–ΓΘΩ
Θ®3Θ©»τ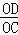 =
=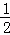 Θ§SΓςOAC=2Θ§«σΥΪ«ζœΏΒΡΫβΈω ΫΘ°
Θ§SΓςOAC=2Θ§«σΥΪ«ζœΏΒΡΫβΈω ΫΘ°
ΓΓ
ΫβΘΚΘ®1Θ©»ΐΘ§kΘΨ0ΘΜ
Θ®2Θ©ΓΏΧί–ΈAOBCΒΡ±ΏOB‘Ύx÷αΒΡ’ΐΑκ÷α…œΘ§ACΓΈOBΘ§BCΓΆOBΘ§
ΓΏΒψCΒΡΉχ±ξΈΣΘ®1Θ§1Θ©Θ§
ΓύAΒψΒΡΉίΉχ±ξΈΣ1Θ§EΒψΒΡΚαΉχ±ξΈΣ1Θ§BΒψΉχ±ξΈΣΘ®1Θ§0Θ©Θ§
Α―y=1¥ζ»κy= ΒΟx=kΘΜΑ―x=1¥ζ»κy=
ΒΟx=kΘΜΑ―x=1¥ζ»κy= ΒΟy=kΘ§
ΒΟy=kΘ§
ΓύAΒψΒΡΉχ±ξΈΣΘ®kΘ§1Θ©Θ§EΒψΒΡΉχ±ξΈΣΘ®1Θ§kΘ©Θ§
ΓύS“θ”Α≤ΩΖ÷=SΓςACE+SΓςOBE
= ΓΝΘ®1﹣kΘ©ΓΝΘ®1﹣kΘ©+
ΓΝΘ®1﹣kΘ©ΓΝΘ®1﹣kΘ©+ ΓΝ1ΓΝkΘ§
ΓΝ1ΓΝkΘ§
= k2﹣
k2﹣ k+
k+ Θ§
Θ§
= Θ®k﹣
Θ®k﹣ Θ©2+
Θ©2+ Θ§
Θ§
Β±k﹣ =0Θ§Φ¥k=
=0Θ§Φ¥k= ±Θ§S“θ”Α≤ΩΖ÷Ήν–ΓΘ§Ήν–Γ÷ΒΈΣ
±Θ§S“θ”Α≤ΩΖ÷Ήν–ΓΘ§Ήν–Γ÷ΒΈΣ ΘΜ
ΘΜ
ΓύEΒψΒΡΉχ±ξ ΈΣΘ®
ΈΣΘ® Θ§1Θ©Θ§Φ¥EΒψΈΣBCΒΡ÷–ΒψΘ§
Θ§1Θ©Θ§Φ¥EΒψΈΣBCΒΡ÷–ΒψΘ§
ΓύΒ±ΒψE‘ΎBCΒΡ÷–Βψ ±Θ§“θ”Α≤ΩΖ÷ΒΡΟφΜΐSΉν–ΓΘΜ
Θ®3Θ©…ηDΒψΉχ±ξΈΣΘ®aΘ§ Θ©Θ§
Θ©Θ§
ΓΏ =
= Θ§
Θ§
Γύ2OD=OCΘ§Φ¥DΒψΈΣOCΒΡ÷–ΒψΘ§
ΓύCΒψΉχ±ξΈΣΘ®2aΘ§ Θ©Θ§
Θ©Θ§
ΓύAΒψΒΡΉίΉχ±ξΈΣ Θ§
Θ§
Α―y= ¥ζ»κy=
¥ζ»κy= ΒΟx=
ΒΟx= Θ§
Θ§
ΓύAΒψΉχ±ξΈΣΘ® Θ§
Θ§ Θ©Θ§
Θ©Θ§
ΓΏSΓςOAC=2Θ§
Γύ ΓΝΘ®2a﹣
ΓΝΘ®2a﹣ Θ©ΓΝ
Θ©ΓΝ =2Θ§
=2Θ§
Γύk= Θ§
Θ§
ΓύΥΪ«ζœΏΒΡΫβΈω ΫΈΣy=

ΓΓ

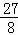 Θ§≤ΔΥΒΟςάμ”…Θ°
Θ§≤ΔΥΒΟςάμ”…Θ°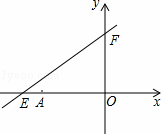

 ﹣
﹣ Θ©Γ¬
Θ©Γ¬ Θ§Τδ÷–Θ§a «ΖΫ≥Χx2
Θ§Τδ÷–Θ§a «ΖΫ≥Χx2 +3x+1=0ΒΡΗυΘ°
+3x+1=0ΒΡΗυΘ°