题目内容
19. 如图,P是平行四边形纸片ABCD的BC边上一点,以过点P的直线为折痕折叠纸片,使点C,D落在纸片所在平面上C′,D′处,折痕与AD边交于点M;再以过点P的直线为折痕折叠纸片,使点B恰好落在C′P边上B′处,折痕与AB边交于点N.若∠MPC=74°,则∠NPB′=16°.
如图,P是平行四边形纸片ABCD的BC边上一点,以过点P的直线为折痕折叠纸片,使点C,D落在纸片所在平面上C′,D′处,折痕与AD边交于点M;再以过点P的直线为折痕折叠纸片,使点B恰好落在C′P边上B′处,折痕与AB边交于点N.若∠MPC=74°,则∠NPB′=16°.
分析 由折叠的性质可求得∠MPC′=∠MPC,∠BPN=∠B′PN,再结合B、P、C在一条直线上,可求得答案.
解答 解:
∵点C,D落在纸片所在平面上C′,D′处,折痕与AD边交于点M,
∴∠MPC′=∠MPC=74°,
∴∠BPB′=180°-∠CPC′=180°-2∠PMC=180°-148°=32°,
∵∠BPN=∠B′PN,
∴∠NPB′=$\frac{1}{2}$∠BPB′=16°,
故答案为:16.
点评 本题主要折叠的性质,掌握折叠前后的线段、角对应相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

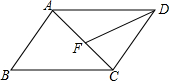 如图,四边形ABCD是平行四边形,∠BAC=80°,DF是∠CDA的角平分线,交AC于点F,∠CDF=25°,则∠CAD=50°.
如图,四边形ABCD是平行四边形,∠BAC=80°,DF是∠CDA的角平分线,交AC于点F,∠CDF=25°,则∠CAD=50°.