题目内容
11.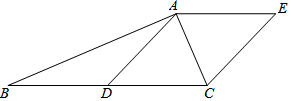 如图,Rt△ABC中,∠BAC=90°,D是BC边的中点,连接AD,过点A作AE∥BC,且AE=CD,连接EC.
如图,Rt△ABC中,∠BAC=90°,D是BC边的中点,连接AD,过点A作AE∥BC,且AE=CD,连接EC.(1)求证:四边形ADCE是菱形;
(2)如果AC=a,tan∠ABC=$\frac{1}{3}$,写出求菱形ADCE的面积的思路.
分析 (1)先证明四边形ADCE是平行四边形,再由直角三角形斜边上的中线性质得出AD=CD,即可得出结论;
(2)由中线的性质得出△ABC的面积=2△ACD的面积,由菱形的性质得出菱形ADCE的面积=2△ACD的面积,得出菱形ADCE的面积=△ABC的面积,由三角函数得出AB=3a,即可求出答案.
解答 (1)证明:∵AE∥BC,AE=CD,
∴四边形ADCE是平行四边形.
∵∠BAC=90°,D是BC边的中点,
∴AD=BD=CD.
∴平行四边形ADCE是菱形.
(2)解:∵D是BC边的中点,
∴△ABC的面积=2△ACD的面积,
∵四边形ADCE是菱形,
∴菱形ADCE的面积=2△ACD的面积,
∴菱形ADCE的面积=△ABC的面积,
∵∠BAC=90°,AC=a,tan∠ABC=$\frac{AC}{AB}$=$\frac{1}{3}$,
∴AB=3AC=3a,
∴菱形ADCE的面积=$\frac{1}{2}$AB•AC=$\frac{3}{2}$a2.
点评 本题考查了菱形的判定与性质、平行四边形的判定、直角三角形斜边上的中线性质、三角函数的运用;熟练掌握菱形的判定与性质是解决问题的关键.

练习册系列答案
相关题目
6.顺义区某中学举行春季运动会,初二年级决定从本年级300名女生中挑选64人组成花束方队,要求身高基本一致,这个工作交给年级学生会体育部小红、小冬和小芳来完成.
为了达到年级的选拔要求,小红、小冬和小芳各自对本学校初二年级的女生身高进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1 小红抽样调查初二年级4名女同学身高统计表(单位:cm)
表2 小冬抽样调查初二年级15名女同学身高统计表(单位:cm)
表3 小芳抽样调查初二年级15名女同学身高统计表(单位:cm)
根据自己的调查数据,小红说应选取身高为163cm(数据的平均数)的同学参加方队,小冬说应选取身高为165cm(数据的中位数)的同学参加方队,小芳说应选取身高为160cm(数据的众数)的同学参加方队.
根据以上材料回答问题:
小红、小冬和小芳三人中,哪一位同学的抽样调查及得出的结论更符合年级的要求,并简要说明符合要求的理由,同时其他两位同学的抽样调查或得出结论的不足之处.
为了达到年级的选拔要求,小红、小冬和小芳各自对本学校初二年级的女生身高进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1 小红抽样调查初二年级4名女同学身高统计表(单位:cm)
| 序号 | 1 | 2 | 3 | 4 |
| 身高 | 155 | 160 | 165 | 172 |
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 身高 | 148 | 149 | 150 | 152 | 152 | 160 | 160 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 175 |
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 身高 | 145 | 160 | 150 | 152 | 160 | 154 | 160 | 166 | 167 | 168 | 160 | 169 | 173 | 174 | 175 |
根据以上材料回答问题:
小红、小冬和小芳三人中,哪一位同学的抽样调查及得出的结论更符合年级的要求,并简要说明符合要求的理由,同时其他两位同学的抽样调查或得出结论的不足之处.
1.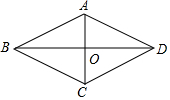 求证:菱形的两条对角线互相垂直.
求证:菱形的两条对角线互相垂直.
已知:如图,四边形ABCD是菱形,对角线AC,BD交于点O.
求证:AC⊥BD.
以下是排乱的证明过程:
①又BO=DO;
②∴AO⊥BD,即AC⊥BD;
③∵四边形ABCD是菱形;
④∴AB=AD.
证明步骤正确的顺序是( )
 求证:菱形的两条对角线互相垂直.
求证:菱形的两条对角线互相垂直.已知:如图,四边形ABCD是菱形,对角线AC,BD交于点O.
求证:AC⊥BD.
以下是排乱的证明过程:
①又BO=DO;
②∴AO⊥BD,即AC⊥BD;
③∵四边形ABCD是菱形;
④∴AB=AD.
证明步骤正确的顺序是( )
| A. | ③→②→①→④ | B. | ③→④→①→② | C. | ①→②→④→③ | D. | ①→④→③→② |
