Question

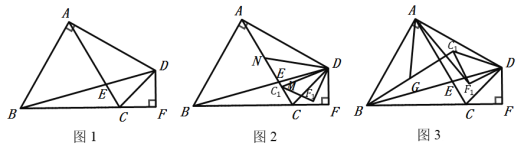
【题目】如图，在平行四边形中，以为圆心，长为半径画弧交于点，分别以点，为圆心，大于的长为半径画弧，两弧交于点，连接AG并延长交于点，连接交于点，过点作于点，连接.若，，则下列结论：①四边形是菱形；②；③；④；⑤.正确的有（　　 ）

A.①③④B.①③⑤C.②③④⑤D.①②③④⑤

Answer 1

【答案】A

【解析】

①根据尺规作图得到直线AE是∠FAB的角平分线，也是线段BF的垂直平分线，根据线段垂直平分线的性质、菱形的判定定理即可判断；②根据菱形的性质，在Rt△ABO中，利用勾股定理可求得AE的长，即可判断；③利用菱形的面积公式“对角线乘积的一半”可求得，即可判断；④根据，可求得的长，即可判断；⑤在Rt△AHE中，根据直角三角形的性质可求得HO的长，即可判断．

①由尺规作图的过程可知，直线AE是∠FAB的角平分线，也是线段BF的垂直平分线，
∴AF=AB，EF=EB，∠FAE=∠BAE，
∵AD∥BC，
∴∠FAE=∠AEB，
∴∠AEB=∠BAE，
∴BA=BE，
∴BA=BE=AF=FE，
∴四边形ABEF是菱形，故①正确；

②∵四边形ABEF是菱形，

∴AE⊥BF，AO=OE，BO=OF=3，

在Rt△ABO中，AB=4，BO =3，∠AOB=90，

∴，

∴AE=2AO=，故②错误；

③∵四边形ABEF是菱形，

∴，故③正确；

④∵四边形ABEF是菱形，

∴BE=AB=4，

∵，

∴，故④正确；

⑤∵四边形ABEF是菱形，

∴O是E的中点，

∴在Rt△AHE中，HO是斜边AE的中线，

∴HO，故⑤错误；

综上，①③④正确，

故选：A．