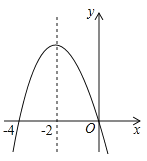��Ŀ����
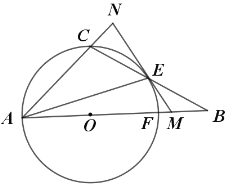
����Ŀ������ΪD��������y����x2+bx+c��x����A��B(3��0)����y���ڵ�C��ֱ��y����![]() x+m������C����x����E(4��0)��
x+m������C����x����E(4��0)��
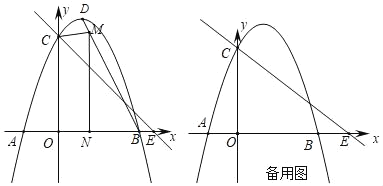
(1)��������ߵĽ���ʽ��
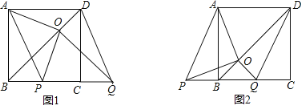
(2)��ͼ1����MΪ�߶�BD�ϲ���B��D�غϵ�һ�����㣬����M��x��Ĵ��ߣ�����ΪN�����M�ĺ�����Ϊx���ı���OCMN�����ΪS����S��x֮��ĺ�����ϵʽ������S�����ֵ��
(3)��PΪx�����������һ�����㣬��P��x��Ĵ��ߣ���ֱ��y����![]() x+m��G������������H������CH������CGH��CH���ۣ�����G�Ķ�Ӧ��Fǡ������y����ʱ����ֱ��д����P�����꣮
x+m��G������������H������CH������CGH��CH���ۣ�����G�Ķ�Ӧ��Fǡ������y����ʱ����ֱ��д����P�����꣮
���𰸡�(1)y����x2+2x+3��(2)S����(x��![]() )2+
)2+![]() ����x��
����x��![]() ʱ��S�����ֵ�����ֵΪ
ʱ��S�����ֵ�����ֵΪ![]() ��(3)���ڣ���P������Ϊ(4��0)��(
��(3)���ڣ���P������Ϊ(4��0)��(![]() ��0).
��0).
��������
��1������E����ֱ�߽���ʽ�У��������C�����꣬����C��B���������߽���ʽ�У�����������߽���ʽ��
��2���������߽���ʽ��ɶ���ʽ���������D�����꣬��ֱ��BD�Ľ���ʽ�������B��D�������ֱ��BD�Ľ���ʽ����MN�ɱ�ʾ����S�ɱ�ʾ��
��3�����P�����꣬���G������ɱ�ʾ����H������ɱ�ʾ��HG���ȿɱ�ʾ�����÷����Ƴ�CG��HG���е�ʽ��⼴�ɣ�
��1������E����ֱ�߽���ʽ�У�
0����![]() ��4+m��
��4+m��
���m��3��
�����ʽΪy����![]() x+3��
x+3��
��C(0��3)��
��B(3��0)��
����![]() ��
��
���![]() ��
��
�������ߵĽ���ʽΪ��y����x2+2x+3��
��2����y����x2+2x+3����(x��1)2+4��
��D(1��4)��
��ֱ��BD�Ľ���ʽΪy��kx+b�������B��D��
![]() ��
��
���![]() ��
��
��ֱ��BD�Ľ���ʽΪy����2x+6��
���M������Ϊ(x����2x+6)��
��S��(3+6��2x)x![]() ����(x��
����(x��![]() )2+
)2+![]() ��
��
�൱x��![]() ʱ��S�����ֵ�����ֵΪ
ʱ��S�����ֵ�����ֵΪ![]() ��
��
(3)���ڣ�
��ͼ��ʾ��
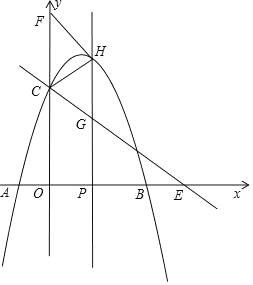
���P������Ϊ(t��0)��
���G(t����![]() t+3)��H(t����t2+2t+3)��
t+3)��H(t����t2+2t+3)��
��HG��|��t2+2t+3��(��![]() t+3)|��|t2��
t+3)|��|t2��![]() t|
t|
CG��![]() ��
��![]() t��
t��
�ߡ�CGH��GH���ۣ�G�Ķ�Ӧ��Ϊ��F��F����y���ϣ�
��HG��y�ᣬ
��HG��CF��HG��HF��CG��CF��
��GHC����CHF��
���FCH����CHG��
���FCH����FHC��
���GCH����GHC��
��CG��HG��
��|t2��![]() t|��
t|��![]() t��
t��
��t2��![]() t��
t��![]() tʱ��
tʱ��
���t1��0(��)��t2��4��
��ʱ��P(4��0)��
��t2��![]() t����
t����![]() tʱ��
tʱ��
���t1��0(��)��t2��![]() ��
��
��ʱ��P(![]() ��0)��
��0)��
���ϣ���P������Ϊ(4��0)��(![]() ��0)��
��0)��