题目内容
12.甲、乙两人同时解方程组$\left\{\begin{array}{l}{mx+y=5①}\\{2x-ny=13②}\end{array}\right.$甲解题看错了①中的m,解得$\left\{\begin{array}{l}{x=\frac{7}{2}}\\{y=-2}\end{array}\right.$,乙解题时看错②中的n,解得$\left\{\begin{array}{l}{x=3}\\{y=-7}\end{array}\right.$,试求原方程组的解.分析 把甲的解代入②中求出n的值,把乙的解代入①中求出m的值;把m与n的值代入方程组求出解即可.
解答 解:(1)把$\left\{\begin{array}{l}{x=\frac{7}{2}}\\{y=-2}\end{array}\right.$代入②得:7+2n=13,
解得:n=3,
把$\left\{\begin{array}{l}{x=3}\\{y=-7}\end{array}\right.$代入①得:3m-7=5,
解得:m=4;
把m=4,n=3代入方程组得:$\left\{\begin{array}{l}{4x+y=5①}\\{2x-3y=13②}\end{array}\right.$,
①×3+②得:14x=28,即x=2,
把x=2代入①得:y=-3,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
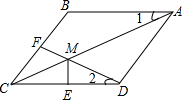 已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.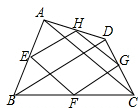 已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,且AC=BD,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).则四边形EFGH的形状是菱形.
已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,且AC=BD,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).则四边形EFGH的形状是菱形. 如图,在△ABC中,AD平分∠BAC,若AB=10cm,AC=8cm,若S△ABD=15,那么S△ACD=12cm2.
如图,在△ABC中,AD平分∠BAC,若AB=10cm,AC=8cm,若S△ABD=15,那么S△ACD=12cm2.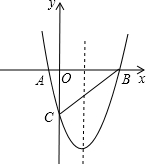 在平面直角坐标系xOy中,抛物线y=x2-4x-5与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
在平面直角坐标系xOy中,抛物线y=x2-4x-5与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.