题目内容
16.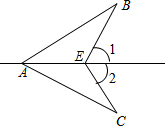 如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件不能是( )
如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件不能是( )| A. | BE=CE | B. | ∠B=∠C | C. | AB=AC | D. | ∠BAE=∠CAE |
分析 根据题意,易得∠AEB=∠AEC,又AE公共边,所以根据全等三角形的判定方法容易寻找添加条件.
解答 解:∵∠1=∠2,
∴∠AEB=∠AEC,
又因为AE公共边,
A、当BE=CE时,符合SAS定理,即此时能推出△ABE≌△ACE,故本选项错误;
B、当∠B=∠C时,符合AAS定理,即此时能推出△ABE≌△ACE,故本选项错误;
C、当AB=AC时,不符合全等三角形的判定定理,不能推出△ABE≌△ACE,故本选项正确;
D、当∠BAE=∠CAE时,符合AAS定理,即此时能推出△ABE≌△ACE,故本选项错误;
故选C.
点评 此题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
7.甲乙两地的海拔高度分别为300米,-50米,那么甲地比乙地高出( )
| A. | 350米 | B. | 50米 | C. | 300米 | D. | 200米 |
11.某种服装进价120元,在试销阶段发现每件售价(元)与产品的日销量(件)始终存在下表中的数量关系:
(1)根据上表所给的数据可知表中的a值是1件.
(2)在不改变上述关系的情况下,当每件定价为多少元时日盈利可达1600元?
| 每件售价(元) | 130 | 150 | 165 | 199 |
| 每日销售量(件) | 70 | 50 | 35 | a |
(2)在不改变上述关系的情况下,当每件定价为多少元时日盈利可达1600元?
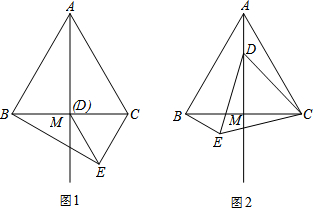
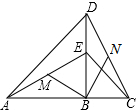 直角△ABD和直角△EBC如图放置,使点A、B、C在一条直线上,∠ABD=∠EBC=90°,AB=DB,EB=CB,M、N分别是AE、CD的中点.
直角△ABD和直角△EBC如图放置,使点A、B、C在一条直线上,∠ABD=∠EBC=90°,AB=DB,EB=CB,M、N分别是AE、CD的中点.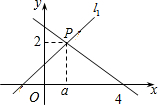 如图,直线l1:y1=x+1与直线l2:y2=mx+n相交于点P(a,2).
如图,直线l1:y1=x+1与直线l2:y2=mx+n相交于点P(a,2). 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.
如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.