题目内容
6.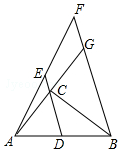 如图,△ABC中,∠C=90°,AC=6,BC=8,点D是AB的中点,点E在DC的延长线上,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.
如图,△ABC中,∠C=90°,AC=6,BC=8,点D是AB的中点,点E在DC的延长线上,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.(1)求证:AC=CG;
(2)若点P是直线BG上的一点,试确定点P的位置,使△BCP与△BCD相似.
分析 (1)利用平行分线段成比例定理即可证明.
(2)分两种情形讨论①如图1中,若∠CDB=∠CPB,②如图2中,若∠PCB=∠CDB,分别求解即可.
解答 证明:∵BF∥DE,
∴$\frac{AD}{DB}$=$\frac{AC}{CG}$,
∵AD=BD,
∴AC=CG.
(2)解:当PB=5或$\frac{64}{5}$时,△BCP与△BCD相似;
在△ABC和△GBC中:
$\left\{\begin{array}{l}{AC=CG}\\{∠ACB=∠GCB}\\{BC=BC}\end{array}\right.$,
∴△ABC≌△GBC(SAS),
∴AB=BG
∴∠DBC=∠CBP,
∵AC=6,BC=8,
∴AB=10,
∴CD=5,
∵∠DBC=∠CBP,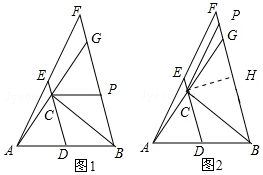
第一种情况:若∠DCB=∠BCP,如图1:
在△BCP与△BCD中
∠DCB=∠BCP,
BC=BC,
∠DBC=∠CBP,
∴△BCP≌△BCD(ASA),
∴BP=CD=5;
第二种情况:若∠PCB=∠DCB,如图2:
∵∠CBD=∠CBP,
∴△BPC∽△BCD,
∴$\frac{BD}{BC}=\frac{BC}{BP}$,
∴BP=$\frac{64}{5}$,
综上所述:当PB=5或$\frac{64}{5}$时,△BCP与△BCD相似.
点评 此题主要考查了相似三角形的判定与性质、全等三角形的判定与性质、勾股定理、直角三角形斜边中线定理、平行线分线段成比例定理等知识,解题的关键是学会用分类讨论的思想思考问题,注意不能漏解,属于中考常考题型.

练习册系列答案
相关题目
1.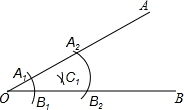 如图,已知∠AOB=30°,以O为圆心、a为半径画弧交OA、OB于A1、B1,再分别以A1、B1为圆心、a为半径画弧交于点C1,以上称为一次操作.再以C1为圆心a为半径重新操作,得到C2.重复以上步骤操作,记最后一个两弧的交点(离点O最远)为CK,则点CK到射线OB的距离为( )
如图,已知∠AOB=30°,以O为圆心、a为半径画弧交OA、OB于A1、B1,再分别以A1、B1为圆心、a为半径画弧交于点C1,以上称为一次操作.再以C1为圆心a为半径重新操作,得到C2.重复以上步骤操作,记最后一个两弧的交点(离点O最远)为CK,则点CK到射线OB的距离为( )
 如图,已知∠AOB=30°,以O为圆心、a为半径画弧交OA、OB于A1、B1,再分别以A1、B1为圆心、a为半径画弧交于点C1,以上称为一次操作.再以C1为圆心a为半径重新操作,得到C2.重复以上步骤操作,记最后一个两弧的交点(离点O最远)为CK,则点CK到射线OB的距离为( )
如图,已知∠AOB=30°,以O为圆心、a为半径画弧交OA、OB于A1、B1,再分别以A1、B1为圆心、a为半径画弧交于点C1,以上称为一次操作.再以C1为圆心a为半径重新操作,得到C2.重复以上步骤操作,记最后一个两弧的交点(离点O最远)为CK,则点CK到射线OB的距离为( )| A. | $\frac{a}{2}$ | B. | $\frac{\sqrt{3}}{2}$a | C. | a | D. | $\sqrt{3}$a |
18.下列哪个式子表示(-x)(-x)(-x)的结果( )
| A. | -3x3 | B. | -3x | C. | -x3 | D. | 3x |
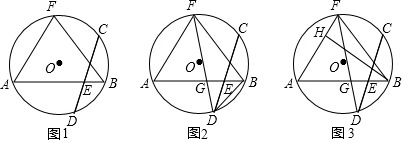
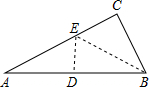 如图把Rt△ABC(∠C=90°)折叠,使A、B两点重合,得到折痕ED,再沿BE折叠,C点恰好与D点重合,则∠ABC等于60度.
如图把Rt△ABC(∠C=90°)折叠,使A、B两点重合,得到折痕ED,再沿BE折叠,C点恰好与D点重合,则∠ABC等于60度.