题目内容
1.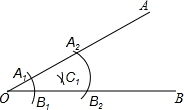 如图,已知∠AOB=30°,以O为圆心、a为半径画弧交OA、OB于A1、B1,再分别以A1、B1为圆心、a为半径画弧交于点C1,以上称为一次操作.再以C1为圆心a为半径重新操作,得到C2.重复以上步骤操作,记最后一个两弧的交点(离点O最远)为CK,则点CK到射线OB的距离为( )
如图,已知∠AOB=30°,以O为圆心、a为半径画弧交OA、OB于A1、B1,再分别以A1、B1为圆心、a为半径画弧交于点C1,以上称为一次操作.再以C1为圆心a为半径重新操作,得到C2.重复以上步骤操作,记最后一个两弧的交点(离点O最远)为CK,则点CK到射线OB的距离为( )| A. | $\frac{a}{2}$ | B. | $\frac{\sqrt{3}}{2}$a | C. | a | D. | $\sqrt{3}$a |
分析 根据作图分别作出C1、C2、C3,由作图可知OB1=B1C1=B2C1=B2C2=B3C2=B3C3=a且∠BOC1=$\frac{1}{2}$∠AOB=15°,利用等边对等角和三角形外角性质得出∠B1OC1=∠B1C1O=15°、∠B1B2C1=∠B2B1C1=30°、∠B2C2C1=∠B2C1C2=45°、∠B2B3C2=∠B3B2C2=60°、∠B3C3C2=∠B3C2C3=75°,利用内角和定理知∠C3B3C2=30°,从而得∠C3B3O=∠C3B3C2+∠B2B3C2=90°,即C3B3⊥OB,即最后一个两弧的交点为C3,从而得出答案.
解答 解:如图所示,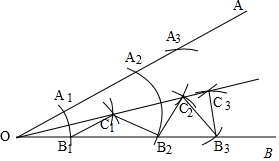
由作图可知OB1=B1C1=B2C1=B2C2=B3C2=B3C3=a,且∠BOC1=$\frac{1}{2}$∠AOB=15°,
∴∠B1OC1=∠B1C1O=15°,
∴∠B1B2C1=∠B2B1C1=∠B1OC1+∠B1C1O=30°,
∴∠B2C2C1=∠B2C1C2=∠B1OC1+∠B1B2C1=45°,
∴∠B2B3C2=∠B3B2C2=∠B1OC1+∠B2C2C1=60°,
∠B3C3C2=∠B3C2C3=∠B1OC1+∠B2B3C2=75°,
则∠C3B3C2=180°-(∠B3C3C2+∠B3C2C3)=30°,
∴∠C3B3O=∠C3B3C2+∠B2B3C2=90°,即C3B3⊥OB,
∴最后一个两弧的交点C3到射线OB的距离为C3B3=a,
故选:C.
点评 本题主要考查角平分线的基本作图,熟练掌握角平分线的基本作图和等边对等角、三角形的外角性质、内角和定理及垂直的定义是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.已知抛物线y=3x2-2的对称轴为( )
| A. | 直线x=2 | B. | 直线 x=-2 | C. | 直线 x=3 | D. | y轴 |
10.在平面直角坐标系中,直线l经过(-3,0),(0,-5)两点,直线l′经过点(2,4)且与y轴平行,则这两条直线的交点位置在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |

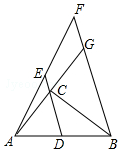 如图,△ABC中,∠C=90°,AC=6,BC=8,点D是AB的中点,点E在DC的延长线上,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.
如图,△ABC中,∠C=90°,AC=6,BC=8,点D是AB的中点,点E在DC的延长线上,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.