题目内容
16．
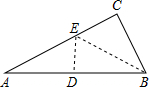如图把Rt△ABC（∠C=90°）折叠，使A、B两点重合，得到折痕ED，再沿BE折叠，C点恰好与D点重合，则∠ABC等于60度．
分析 由折叠的性质知，AD=BD=BC，可求得sinA=$\frac{1}{2}$，所以可得∠A=30°，进而求得结论．
解答 解：根据折叠的性质得AD=BD=BC．
∴sinA=BC：AB=$\frac{1}{2}$，
∴∠A=30°，
∴∠ABC=90°-∠A=60°，
故答案为：60．
点评 本题考查了翻折变换-折叠，特殊角的三角函数，熟记特殊角的三角函数值是解题的关键．
练习册系列答案
相关题目
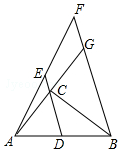如图，△ABC中，∠C=90°，AC=6，BC=8，点D是AB的中点，点E在DC的延长线上，过点B作BF∥DE交AE的延长线于点F，交AC的延长线于点G．
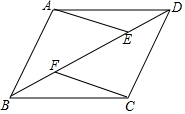如图，?ABCD中，点E、F在BD上，且BF=DE．
如图，平行四边形ABCD中，E是CD的延长线上一点，BE与AD交于点F，DE=$\frac{1}{2}$CD．求证：△ABF∽△CEB．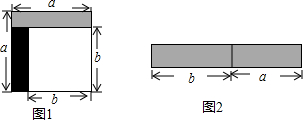
从边长为a的正方形中剪掉一个边长为b的正方形（如图1），然后将剩余部分拼成一个长方形（如图2）．
5．
如图，在平面直角坐标系xOy中，直线y=$\frac{3}{2}$x与双曲线y=$\frac{6}{x}$相交于A，B两点，C是第一象限内双曲线上一点，连接CA并延长交y轴于点P，连接BP，BC．若△PBC的面积是20，则点C的坐标为（ ）
如图，在平面直角坐标系xOy中，直线y=$\frac{3}{2}$x与双曲线y=$\frac{6}{x}$相交于A，B两点，C是第一象限内双曲线上一点，连接CA并延长交y轴于点P，连接BP，BC．若△PBC的面积是20，则点C的坐标为（ ）| A． | （$\frac{14}{3}$，$\frac{9}{7}$） | B． | （4，$\frac{3}{2}$） | C． | （5，$\frac{6}{5}$） | D． | （$\frac{16}{3}$，$\frac{9}{8}$） |
如图，BE⊥CD于点E，CE=AE，BC=DA