题目内容
3.已知a=$\sqrt{5}$+1,b=$\sqrt{5}$-1,求下列各式的值:(1)a2+2ab+b2;
(2)a2b+ab2.
分析 (1)利用完全平方公式化成(a+b)2的形式,然后代入求解;
(2)分解因式化成ab(a+b)的形式,然后代入求值.
解答 解:(1)原式=(a+b)2=[($\sqrt{5}$+1)+($\sqrt{5}$-1)][($\sqrt{5}$+1)-($\sqrt{5}$-1)]=2$\sqrt{5}$×2=4$\sqrt{5}$;
(2)原式=ab(a+b)=($\sqrt{5}$+1)($\sqrt{5}$-1)[($\sqrt{5}$+1)+($\sqrt{5}$-1)]=4×2$\sqrt{5}$=8$\sqrt{5}$.
点评 本题考查了二次根式的化简求值,正确对所求的式子分解因式是关键.

练习册系列答案
相关题目
15.已知抛物线y=3x2-2的对称轴为( )
| A. | 直线x=2 | B. | 直线 x=-2 | C. | 直线 x=3 | D. | y轴 |
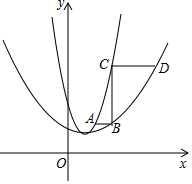 若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.
若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.
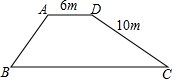 如图是一座堤坝的横断面,AB坡坡角为45°,DC坡坡度为1:2,其他数据如图所示,求BC的长(精确到0.1m).(参考数据:$\sqrt{2}$≈1.414,$\sqrt{5}$≈2.236)
如图是一座堤坝的横断面,AB坡坡角为45°,DC坡坡度为1:2,其他数据如图所示,求BC的长(精确到0.1m).(参考数据:$\sqrt{2}$≈1.414,$\sqrt{5}$≈2.236)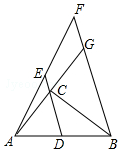 如图,△ABC中,∠C=90°,AC=6,BC=8,点D是AB的中点,点E在DC的延长线上,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.
如图,△ABC中,∠C=90°,AC=6,BC=8,点D是AB的中点,点E在DC的延长线上,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.