��Ŀ����
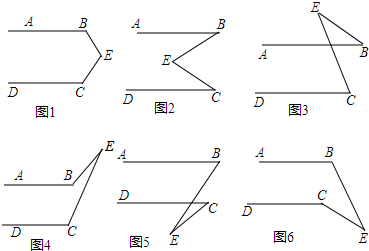
4����ͼ���ڡ�ABC�У���C=90�㣬������CDEF�Ķ���D�ڱ�AC�ϣ���F������CB�ϣ���CD=x��������CDEF���ABC�ص����ֵ����ΪS��S����x�ĺ���ͼ����ͼ��ʾ������0��x��m��m��x��2��2��x��n�������Ľ���ʽ��ͬ����1����գ�m��ֵΪ$\frac{3}{2}$��
��2����S����x�ĺ�������ʽ����д��x��ȡֵ��Χ��
��3��S��ֵ�ܷ�Ϊ5�����ܣ������ʱx��ֵ�������ܣ�˵�����ɣ�
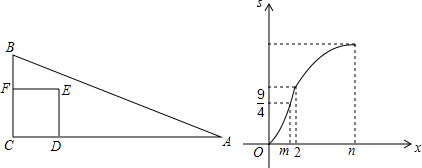
���� ��1������ͼ����Ϣ�г����̣�m2=$\frac{9}{4}$���ɽ����
��2���������������ۣ���0��x��$\frac{3}{2}$����$\frac{3}{2}$��x��2����2��x��6���ֱ�ͼ�����s��x�Ĺ�ϵ���ɣ�
��3�����ã�2���Ľ����г����̽�����ɣ�
��� �⣺��1����0��x��mʱ����Ȼ���������������ڣ�
��ʱS=CD•CF=x2��
��S=$\frac{9}{4}$����$\frac{9}{4}$=m2��
��ã�m=$\frac{3}{2}$����m=-$\frac{3}{2}$����ȥ����
�ʴ�Ϊ��$\frac{3}{2}$��
��2�����S����x�ĺ���ͼ��仯��֪��
BC=2����CD=DE=$\frac{3}{2}$ʱ����E���߶�AB�ϣ�
��DE��BC��
���ADE�ס�ACB��
��$\frac{AD}{AC}=\frac{DE}{CB}$����$\frac{AC-\frac{3}{2}}{AC}=\frac{\frac{3}{2}}{2}$��
��ã�AC=6��
��n=6��
�ٵ�0��x��$\frac{3}{2}$ʱ��S=x2��
�ڵ�$\frac{3}{2}$��x��2ʱ����ͼ1�У�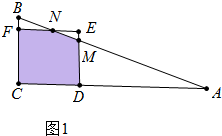
��DM��BC��
��$\frac{DM}{CB}$=$\frac{AD}{AC}$��
��$\frac{DM}{2}$=$\frac{6-x}{6}$��
��DM=$\frac{1}{3}$��6-x����EM=ED-DM=$\frac{4}{3}$x-2��
�ɡ�NEM�ס�ACB�õ�$\frac{NE}{AC}=\frac{EM}{BC}$����NE=3EM=4x-6��
��s=S������CDEF-S��MNE=x2-$\frac{��4x-6��^{2}}{6}$��
��2��x��6ʱ����ͼ2�У�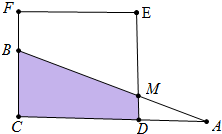
s=S��ABC-S��ADM=6-$\frac{1}{2}$•$\frac{1}{3}$��6-x��•��6-x��=6-$\frac{��6-x��^{2}}{6}$��
��������s=$\left\{\begin{array}{l}{{x}^{2}}&{��0��x��\frac{3}{2}��}\\{{x}^{2}-\frac{��4x-6��^{2}}{6}}&{��\frac{3}{2}��x��2��}\\{6-\frac{��6-x��^{2}}{6}}&{��2��x��6��}\end{array}\right.$��
��3����ͼ���֪O��x��2ʱ��s������Ϊ5��
��6-$\frac{��6-x��^{2}}{6}$=5��
�ࣨ6-x��2=6��
��x=6-$\sqrt{6}$����6+$\sqrt{6}$����������������
��x=6-$\sqrt{6}$ʱ��s=5��
���� ���⿼�鶯������ĺ���ͼ�����⡢�����ε����ʡ����������ε��ж������ʡ������������֪ʶ���ۺ��ԱȽ�ǿ����Ҫ��ȷ����ͼ�Σ��ֶ����ۣ�����Ĺؼ��������������ε����ʣ������Ӧ���߶Σ������п��������ͣ�

 ������������ϵ�д�
������������ϵ�д� ��ͼ����OΪ��ABC�����Բ��ABΪ��O��ֱ�����ӳ�AB����E������EC���ҡ�BCE=��BAC��
��ͼ����OΪ��ABC�����Բ��ABΪ��O��ֱ�����ӳ�AB����E������EC���ҡ�BCE=��BAC��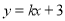 ������A��-1,2������X�ύ�ڵ�B����B�������ǣ� ��
������A��-1,2������X�ύ�ڵ�B����B�������ǣ� ��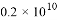 B.
B. 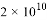 C.
C. 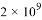 D.
D. 
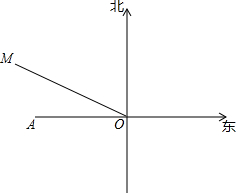 ��ͼ����������Ԥ����̨������λ��A����������300km�ĵ�O��������20km/h���ٶ���ƫ��60�㷽���ƶ�������̨������250km��Χ�ڶ����ܵ�Ӱ�죬��̨���ƶ����ٶȺͷ��䣬��A����̨��Ӱ���ʱ�����ж��
��ͼ����������Ԥ����̨������λ��A����������300km�ĵ�O��������20km/h���ٶ���ƫ��60�㷽���ƶ�������̨������250km��Χ�ڶ����ܵ�Ӱ�죬��̨���ƶ����ٶȺͷ��䣬��A����̨��Ӱ���ʱ�����ж��