题目内容
2. 如图,△ABC中,∠A=40°,∠B=80°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,求∠CDF的度数.
如图,△ABC中,∠A=40°,∠B=80°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,求∠CDF的度数.
分析 首先根据三角形的内角和定理求得∠ACB的度数,以及∠BCD的度数,根据角的平分线的定义求得∠BCE的度数,则∠ECD可以求解,然后在△CDF中,利用内角和定理即可求得∠CDF的度数.
解答 解:∵∠A=40°,∠B=80°,
∴∠ACB=180°-∠A-∠B=60°,
∵CE平分∠ACB,
∴∠ACE=$\frac{1}{2}$∠ACB=30°,
∵CD⊥AB于D,
∴∠CDA=90°,
∠ACD=180°-∠A-∠CDA=50°,
∴∠ECD=∠ACD-∠ACE=20°,
∵DF⊥CE,
∴∠CFD=90°,
∴∠CDF=180°-∠CFD-∠DCE=70°.
点评 本题考查了三角形的内角和等于180°以及角平分线的定义,是基础题,准确识别图形是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.甲、乙两人各射靶10次,他们命中环数的平均成绩为7环,但方差不同,S甲2=2.5,S乙2=1.8,那么( )
| A. | 甲的波动比乙的波动大 | B. | 乙的波动比甲的波动大 | ||
| C. | 甲、乙的波动大小一样 | D. | 甲、乙的波动大小无法确定 |
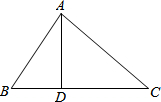 如图,在△ABC中,D是BC边上一点,AB=13,AD=12,BD=5,CD=9,求AC的长.
如图,在△ABC中,D是BC边上一点,AB=13,AD=12,BD=5,CD=9,求AC的长. 如图,某公司组织员工假期去旅游,租用了一辆耗油量为每百公里约为25L的大巴车,大巴车出发前油箱有油100L,大巴车的平均速度为80km/h,行驶若干小时后,由于害怕油箱中的油不够,在途中加了一次油,油箱中剩余油量y(L)与行驶时间x(h)之间的关系如图所示,请根据图象回答下列问题:
如图,某公司组织员工假期去旅游,租用了一辆耗油量为每百公里约为25L的大巴车,大巴车出发前油箱有油100L,大巴车的平均速度为80km/h,行驶若干小时后,由于害怕油箱中的油不够,在途中加了一次油,油箱中剩余油量y(L)与行驶时间x(h)之间的关系如图所示,请根据图象回答下列问题: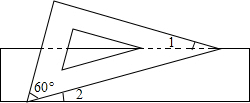 如图,有一块含有60°角的直角三角板的两个顶点放在矩形的对边上.如果∠1=15°,那么∠2的度数是15°.
如图,有一块含有60°角的直角三角板的两个顶点放在矩形的对边上.如果∠1=15°,那么∠2的度数是15°. 如图,要判定AB∥CD,可以添加的条件是∠2=∠5(写一个即可).
如图,要判定AB∥CD,可以添加的条件是∠2=∠5(写一个即可). 先阅读然后回答问题:
先阅读然后回答问题: 如图所示的数阵叫“莱布尼兹调和三角形”,它是由整数的倒数组成的,第n行有n个数,且两端的数都为$\frac{1}{n}$,每个数是它下一行左右相邻两数的和,则第8行第3个数(从左往右数)为$\frac{1}{168}$.
如图所示的数阵叫“莱布尼兹调和三角形”,它是由整数的倒数组成的,第n行有n个数,且两端的数都为$\frac{1}{n}$,每个数是它下一行左右相邻两数的和,则第8行第3个数(从左往右数)为$\frac{1}{168}$.