题目内容
14. 如图所示的数阵叫“莱布尼兹调和三角形”,它是由整数的倒数组成的,第n行有n个数,且两端的数都为$\frac{1}{n}$,每个数是它下一行左右相邻两数的和,则第8行第3个数(从左往右数)为$\frac{1}{168}$.
如图所示的数阵叫“莱布尼兹调和三角形”,它是由整数的倒数组成的,第n行有n个数,且两端的数都为$\frac{1}{n}$,每个数是它下一行左右相邻两数的和,则第8行第3个数(从左往右数)为$\frac{1}{168}$.
分析 观察图中三角形的数阵,将其改写成等阶形式,发现分母的规律,第n行第k项的通项是$\frac{1}{{kC}_{n}^{k}}$,由此得出第8行第3个数.
解答 解:图中三角形的数阵,将其改写成等阶形式:
$\frac{1}{{C}_{1}^{1}}$,
$\frac{1}{{C}_{2}^{1}}$,$\frac{1}{{2C}_{2}^{2}}$,
$\frac{1}{{C}_{3}^{1}}$,$\frac{1}{{2C}_{3}^{2}}$,$\frac{1}{{3C}_{3}^{3}}$,
$\frac{1}{{C}_{4}^{1}}$,$\frac{1}{{2C}_{4}^{2}}$,$\frac{1}{{3C}_{4}^{3}}$,$\frac{1}{{4C}_{4}^{4}}$,
…
因此,第n行第k项的通项是$\frac{1}{{kC}_{n}^{k}}$,故第8行第3个数是$\frac{1}{{3C}_{8}^{3}}$=$\frac{1}{3×\frac{8×7×6}{3×2×1}}$=$\frac{1}{168}$,
故答案为:$\frac{1}{168}$.
点评 本题主要考查了数字的变化规律,根据已知归纳规律,运用规律是解答此题的关键.

练习册系列答案
相关题目
3.若分式$\frac{{{x^2}-1}}{x+1}$的值为0,则x的值为( )
| A. | -1 | B. | 1 | C. | ±1 | D. | 2 |
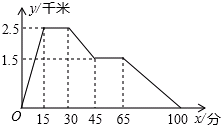 下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.其中x表示时间,y表示张强离家的距离.根据图象回答下列问题:
下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.其中x表示时间,y表示张强离家的距离.根据图象回答下列问题: 如图,△ABC中,∠A=40°,∠B=80°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,求∠CDF的度数.
如图,△ABC中,∠A=40°,∠B=80°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,求∠CDF的度数. 如图,将三角板的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,∠3等于70度.
如图,将三角板的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,∠3等于70度.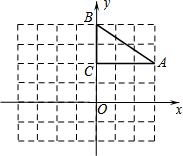 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立了平面直角坐标系后,△ABC的三个顶点都在格点上,将△ABC绕(0,1)点逆时针方向旋转90°,得到△A′B′C′.
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立了平面直角坐标系后,△ABC的三个顶点都在格点上,将△ABC绕(0,1)点逆时针方向旋转90°,得到△A′B′C′.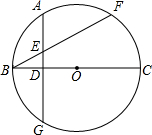 (1)已知抛物线的顶点为(-1,2),且过点(1,-6),求这个函数的表达式;
(1)已知抛物线的顶点为(-1,2),且过点(1,-6),求这个函数的表达式;