题目内容
14.已知:非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,在下列条件中,不能判定$\overrightarrow{a}$∥$\overrightarrow{b}$的是( )| A. | $\overrightarrow{a}$∥$\overrightarrow{c}$,$\overrightarrow{b}$∥$\overrightarrow{c}$ | B. | $\overrightarrow{a}$=2$\overrightarrow{c}$,$\overrightarrow{b}$=$\overrightarrow{c}$ | C. | $\overrightarrow{a}$=-5$\overrightarrow{b}$ | D. | |$\overrightarrow{a}$|=2|$\overrightarrow{b}$| |
分析 根据向量的性质进行逐一判定即可.
解答 解:A、由于$\overrightarrow{a}$∥$\overrightarrow{c}$,所以$\overrightarrow{a}$与$\overrightarrow{c}$的方向相同,由于$\overrightarrow{b}$∥$\overrightarrow{c}$,所以$\overrightarrow{b}$与$\overrightarrow{c}$的方向相同,所以$\overrightarrow{a}$∥$\overrightarrow{b}$,故本选项不符合题意;
B、因为$\overrightarrow{a}$=2$\overrightarrow{c}$,所以$\overrightarrow{a}$与2$\overrightarrow{c}$的方向相同,由于$\overrightarrow{b}$=$\overrightarrow{c}$,所以$\overrightarrow{b}$与$\overrightarrow{c}$的方向相同,所以$\overrightarrow{a}$∥$\overrightarrow{b}$,故本选项不符合题意;
C、因为$\overrightarrow{a}$=-5$\overrightarrow{b}$,所以$\overrightarrow{a}$与$\overrightarrow{b}$的方向相反,所以$\overrightarrow{a}$∥$\overrightarrow{b}$,故本选项不符合题意;
D、因为|$\overrightarrow{a}$|=2|$\overrightarrow{b}$|,所以$\overrightarrow{a}$与$\overrightarrow{b}$的方向不能确定,故不能判定其位置关系,故本选项符合题意.
故选D.
点评 本题考查的是向量中平行向量的定义,即方向相同或相反的非零向量a、b叫做平行向量.

| A. | 0 | B. | -1 | C. | 0或-1 | D. | 1或-1 |
 如图所示,此图的俯视图为( )
如图所示,此图的俯视图为( )| A. |  | B. |  | C. |  | D. |  |
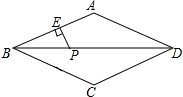 如图,P是菱形ABCD对角线BD上一点,PE⊥AB于E,PE=4cm,则点P到BC的距离是( )
如图,P是菱形ABCD对角线BD上一点,PE⊥AB于E,PE=4cm,则点P到BC的距离是( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 8cm |
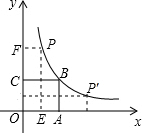 如图,正方形OABC的面积为16,点O为坐标原点,点B在双曲线y=$\frac{k}{x}$(x>0)上,点P(m,n)是双曲线上任意一点,过点P分别作x轴、y轴的垂线,垂足分别为E、F,并设矩形OEPF在正方形OABC之外部分的面积为S.
如图,正方形OABC的面积为16,点O为坐标原点,点B在双曲线y=$\frac{k}{x}$(x>0)上,点P(m,n)是双曲线上任意一点,过点P分别作x轴、y轴的垂线,垂足分别为E、F,并设矩形OEPF在正方形OABC之外部分的面积为S.