题目内容
5.若关于x的方程$\frac{x-1}{x-2}-\frac{m}{2-x}$=m无解,则m的值为( )| A. | 0 | B. | -1 | C. | 0或-1 | D. | 1或-1 |
分析 分式方程无解的条件是:去分母后所得整式方程无解,或解这个整式方程得到的解使原方程的分母等于0.
解答 解:方程去分母,得:x-1+m=m(x-2),
(1-m)x=1-3m,
当1-m=0时,整式方程无解,即m=1;
当x-2=0时,即x=2,分式方程无解,
把x=2代入(1-m)x=1-3m得:2(1-m)=1-3m,
解得:m=-1,
∴m=1或-1,
故选:D.
点评 本题考查了分式方程的解,解决本题的关键是明确分式方程无解的条件.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.在下列方程中,没有实数根的是( )
| A. | x2+2x-1=0 | B. | x2+2$\sqrt{2}$x+2=0 | C. | x2+$\sqrt{2}$x+1=0 | D. | -x2+2x+2=0 |
14.已知:非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,在下列条件中,不能判定$\overrightarrow{a}$∥$\overrightarrow{b}$的是( )
| A. | $\overrightarrow{a}$∥$\overrightarrow{c}$,$\overrightarrow{b}$∥$\overrightarrow{c}$ | B. | $\overrightarrow{a}$=2$\overrightarrow{c}$,$\overrightarrow{b}$=$\overrightarrow{c}$ | C. | $\overrightarrow{a}$=-5$\overrightarrow{b}$ | D. | |$\overrightarrow{a}$|=2|$\overrightarrow{b}$| |
 图中∠AED分别为△ADE,△ABE中AD,AB边所对的角,在△AFD中,∠AFD是边AF,ED组成的角.
图中∠AED分别为△ADE,△ABE中AD,AB边所对的角,在△AFD中,∠AFD是边AF,ED组成的角.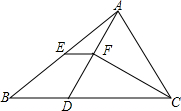 如图,在△ABC中,D在BC上,且CD=CA,CF平分∠ACB,AE=EB
如图,在△ABC中,D在BC上,且CD=CA,CF平分∠ACB,AE=EB