题目内容
6.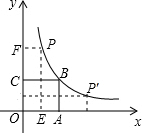 如图,正方形OABC的面积为16,点O为坐标原点,点B在双曲线y=$\frac{k}{x}$(x>0)上,点P(m,n)是双曲线上任意一点,过点P分别作x轴、y轴的垂线,垂足分别为E、F,并设矩形OEPF在正方形OABC之外部分的面积为S.
如图,正方形OABC的面积为16,点O为坐标原点,点B在双曲线y=$\frac{k}{x}$(x>0)上,点P(m,n)是双曲线上任意一点,过点P分别作x轴、y轴的垂线,垂足分别为E、F,并设矩形OEPF在正方形OABC之外部分的面积为S.(1)求B点坐标和k的值;
(2)当S=8时,求点P的坐标;
(3)写出S与m的函数关系式.
分析 (1)先求出正方形的边长,然后根据反比例函数图象在第一象限写出点B的坐标,再根据待定系数法列式即可求出k值;
(2)①当点P在点B的左边时,矩形OEPF在正方形OABC之外部分的面积为m(n-4),再根据反比例函数的性质,进行计算即可求解,②当点P在点B的右边时,矩形OEPF在正方形OABC之外部分的面积为4(4-n),再根据反比例函数的性质,进行计算即可求解;
(3)分点P在点B的左边与右边两种情况,结合反比例函数的性质,消去字母n,整理即可得到S与m的函数关系式.
解答 解:(1)∵正方形OABC的面积为16,
∴OA=OC=4,
∴B(4,4),
又∵点B(4,4)在函数$y=\frac{k}{x}$的图象上,
∴k=16;
故点B的坐标是(4,4),k=16;
(2)分两种情况:
①当点P在点B的左侧时,
∵P(m,n)在函数y=$\frac{k}{x}$上,
∴mn=16,
∴S=m(n-4)=mn-4m=8,
解得m=2,
∴n=8,
∴点P的坐标是P(2,8);
②当点P在点B的右侧时,
∵P(m,n)在函数y=$\frac{k}{x}$上,
∴mn=16,
∴S=4(4-n)=16-4n=8,
解得n=2,
∴$\frac{16}{m}$=2,
解得m=8,
∴点P的坐标是P(8,2),
综上所述:P(2,8),(8,2).
(3)当0<m<4时,点P在点B的左边,此时S=16-4m,
当m≥4时,点P在点B的右边,此时S=16-4n=16-4×$\frac{16}{m}$=16-$\frac{64}{m}$.
点评 本题主要考查了反比例函数的系数与矩形的面积的关系,把线段的长的问题转化为点的坐标问题是解决本题的关键,需要注意分点P在点B的左边与右边两种情况,并且不重叠部分有两部分,进行讨论求解,避免漏解而导致出错.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案| A. | $\overrightarrow{a}$∥$\overrightarrow{c}$,$\overrightarrow{b}$∥$\overrightarrow{c}$ | B. | $\overrightarrow{a}$=2$\overrightarrow{c}$,$\overrightarrow{b}$=$\overrightarrow{c}$ | C. | $\overrightarrow{a}$=-5$\overrightarrow{b}$ | D. | |$\overrightarrow{a}$|=2|$\overrightarrow{b}$| |
| A. | y=$\frac{1}{9x}$ | B. | $\frac{y}{2x}=1$ | C. | y=-3x2 | D. | $\frac{1}{5}$xy=-2 |
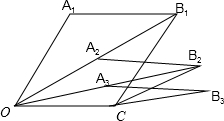 如图所示,平行四边形OA1B1C中,OA1=OC=1,∠A1OC=60°,记为第一个平行四边形,A2是对角线OB1的中点,以OA2和OC为边,再做平行四边形OA2B2C,依此类推,第三个平行四边形的面积为$\frac{\sqrt{3}}{8}$;第n个平行四边形的面积为$\frac{\sqrt{3}}{{2}^{n}}$.
如图所示,平行四边形OA1B1C中,OA1=OC=1,∠A1OC=60°,记为第一个平行四边形,A2是对角线OB1的中点,以OA2和OC为边,再做平行四边形OA2B2C,依此类推,第三个平行四边形的面积为$\frac{\sqrt{3}}{8}$;第n个平行四边形的面积为$\frac{\sqrt{3}}{{2}^{n}}$. 将一张长方形纸片按如图所示折叠,如果∠1=58°,那么∠2=64°.
将一张长方形纸片按如图所示折叠,如果∠1=58°,那么∠2=64°.