题目内容
3.我们已经学习了一元二次方程的三种解法:因式分解法,配方法和公式法.请选择你认为适当的方法解下列方程.①x2-3x+1=0;②x2-3x=0;③x2-2x=4.
分析 ①利用求根公式法解方程;
②利用因式分解法解方程;
③利用配方法解方程.
解答 解:①△=(-3)2-4×1×1=5,
x=$\frac{3±\sqrt{5}}{2}$,
所以x1=$\frac{3+\sqrt{5}}{2}$,x2=$\frac{3-\sqrt{5}}{2}$;
②x(x-3)=0,
x=0或x-3=0,
所以x1=0,x2=3;
③x2-2x+1=4+1,
(x-1)2=5,
x-1=±$\sqrt{5}$,
所以x1=1+$\sqrt{5}$,x2=1-$\sqrt{5}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了配方法和公式法解一元二次方程.

练习册系列答案
相关题目
14.已知:非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,在下列条件中,不能判定$\overrightarrow{a}$∥$\overrightarrow{b}$的是( )
| A. | $\overrightarrow{a}$∥$\overrightarrow{c}$,$\overrightarrow{b}$∥$\overrightarrow{c}$ | B. | $\overrightarrow{a}$=2$\overrightarrow{c}$,$\overrightarrow{b}$=$\overrightarrow{c}$ | C. | $\overrightarrow{a}$=-5$\overrightarrow{b}$ | D. | |$\overrightarrow{a}$|=2|$\overrightarrow{b}$| |
8.小明家冰箱冷冻室温度为-6℃,此时房屋内的温度为10℃,则房屋内的温度比冰箱冷冻室的温度高( )
| A. | 16℃ | B. | 4℃ | C. | -16℃ | D. | -4℃ |
 将一张长方形纸片按如图所示折叠,如果∠1=58°,那么∠2=64°.
将一张长方形纸片按如图所示折叠,如果∠1=58°,那么∠2=64°.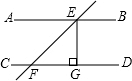 如图,已知直线AB∥CD,直线EF截AB、CD于E、F,EG⊥CD,∠EFD=45°且FG=6,则AB、CD之间的距离为6.
如图,已知直线AB∥CD,直线EF截AB、CD于E、F,EG⊥CD,∠EFD=45°且FG=6,则AB、CD之间的距离为6.