题目内容
20.已知抛物线y=ax2+bx+3的对称轴是直线x=1.(1)求证:2a+b=0;
(2)抛物线与y轴交于点A,求点A关于直线x=1的对称点坐标.
分析 (1)直接利用对称轴公式代入求出即可;
(2)求得与y轴的交点坐标后即可求得关于直线x=1的对称点的坐标.
解答 (1)证明:∵对称轴是直线x=1=-$\frac{b}{2a}$,
∴2a+b=0;
(2)令x=0,得:y=3,
∴抛物线y=ax2+bx+3与y轴交于(0,3),
∴点(0,3)关于直线x=1的对称点的坐标为(2,3).
点评 此题考查了二次函数的性质及对称的知识,解题的关键是能够了解对称点的知识,难度不大.

练习册系列答案
相关题目
15.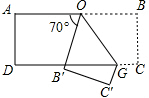 如图,把一张长方形的纸按如图所示那样折叠,B、C两点分别落在B′,C′点处,若∠AOB′=70°,则∠B′OG的度数为( )
如图,把一张长方形的纸按如图所示那样折叠,B、C两点分别落在B′,C′点处,若∠AOB′=70°,则∠B′OG的度数为( )
 如图,把一张长方形的纸按如图所示那样折叠,B、C两点分别落在B′,C′点处,若∠AOB′=70°,则∠B′OG的度数为( )
如图,把一张长方形的纸按如图所示那样折叠,B、C两点分别落在B′,C′点处,若∠AOB′=70°,则∠B′OG的度数为( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
12.下列各图中,属于轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.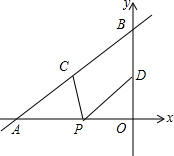 如图,直线y=$\frac{2}{3}$x+4与x轴,y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,则PC+PD的最小值为( )
如图,直线y=$\frac{2}{3}$x+4与x轴,y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,则PC+PD的最小值为( )
 如图,直线y=$\frac{2}{3}$x+4与x轴,y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,则PC+PD的最小值为( )
如图,直线y=$\frac{2}{3}$x+4与x轴,y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,则PC+PD的最小值为( )| A. | 2+$\sqrt{13}$ | B. | 5 | C. | 2$\sqrt{13}$ | D. | 6 |

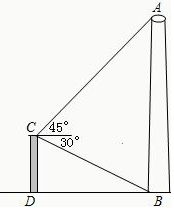 如图,在城市改造时,要拆除建筑物AB,在离它21米远的建筑物CD顶端C测得A的仰角45°,B的俯角30°,在点B的35米处有一文物,问:此文物是否在危险区内?请说明理由.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,在城市改造时,要拆除建筑物AB,在离它21米远的建筑物CD顶端C测得A的仰角45°,B的俯角30°,在点B的35米处有一文物,问:此文物是否在危险区内?请说明理由.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732) 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.