题目内容
10.分式$\frac{x}{6a{b}^{2}}$,$\frac{y}{9{a}^{2}bc}$最简公分母是18a2b2c;分式$\frac{1}{{x}^{2}-3x}$,$\frac{1}{{x}^{2}-9}$最简公分母是x(x-3)(x+3).分析 分母是多项式的先因式分解,然后再找出最简公分母.
解答 解:分式$\frac{x}{6a{b}^{2}}$,$\frac{y}{9{a}^{2}bc}$最简公母为:18a2b2c,
分式$\frac{1}{{x}^{2}-3x}$,$\frac{1}{{x}^{2}-9}$可化为:$\frac{1}{x(x-3)}$,$\frac{1}{(x-3)(x+3)}$,
∴最简公分母为:x(x-3)(x+3)
故答案为:18a2b2c,x(x-3)(x+3)
点评 本题考查最简公分母,涉及因式分解,分式的基本性质,本题属于基础题型.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
1.下列事件是随机事件的是( )
| A. | 人长生不老 | |
| B. | 2016年奥运会中国队获100枚金牌 | |
| C. | 掷两枚质地均匀的正方体骰子朝上一面的点数之积为21 | |
| D. | 一个星期为七天 |
18.关于一次函数y=x-1,下列说法:①图象与y轴的交点坐标是(0,-1);②y随x的增大而增大;③图象经过第一、二、三象限; ④直线y=x-1可以看作由直线y=x向右平移1个单位得到.其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.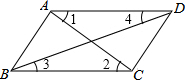 如图,下列四组条件中,能判定AB∥CD的是( )
如图,下列四组条件中,能判定AB∥CD的是( )
 如图,下列四组条件中,能判定AB∥CD的是( )
如图,下列四组条件中,能判定AB∥CD的是( )| A. | ∠1=∠2 | B. | ∠BAD+∠ADC=180° | C. | ∠3=∠4 | D. | ∠BAD+∠ABC=180° |
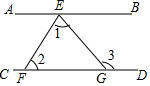 如图,AB∥CD,E是直线AB上的一点,F,G分别是直线CD上的两点,试说明∠3=∠1+∠2.
如图,AB∥CD,E是直线AB上的一点,F,G分别是直线CD上的两点,试说明∠3=∠1+∠2.