题目内容
8.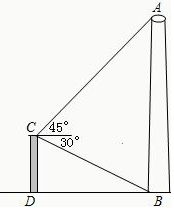 如图,在城市改造时,要拆除建筑物AB,在离它21米远的建筑物CD顶端C测得A的仰角45°,B的俯角30°,在点B的35米处有一文物,问:此文物是否在危险区内?请说明理由.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,在城市改造时,要拆除建筑物AB,在离它21米远的建筑物CD顶端C测得A的仰角45°,B的俯角30°,在点B的35米处有一文物,问:此文物是否在危险区内?请说明理由.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
分析 首先分析图形:根据题意构造直角三角形;本题涉及多个直角三角形,应利用其公共边构造等量关系,进而可求出答案.
解答 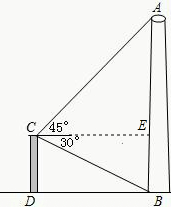 答:文物不在危险区内.
答:文物不在危险区内.
解:在Rt△AEC中,∠ACE=45°,
则CE=EA,
∵DB=CE=21m,
∴DB=EA=21m,
在Rt△CEB中,∠BCE=30°,
则tan30°=$\frac{BE}{EC}$,即BE=ECtan30°,
∴BE=21×$\frac{\sqrt{3}}{3}$=7$\sqrt{3}$m,
∴AB=AE+EB=(21+7$\sqrt{3}$)m,
∵AB=(21+7$\sqrt{3}$)<35,
∴文物不在危险区内.
点评 本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
18.关于一次函数y=x-1,下列说法:①图象与y轴的交点坐标是(0,-1);②y随x的增大而增大;③图象经过第一、二、三象限; ④直线y=x-1可以看作由直线y=x向右平移1个单位得到.其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.若要使分式$\frac{2x+2}{{{{({x+1})}^2}}}$的值为整数,则整数x可取的个数为( )
| A. | 5个 | B. | 2个 | C. | 3个 | D. | 4个 |
3. 图中包含了( )个小于平角的角.
图中包含了( )个小于平角的角.
 图中包含了( )个小于平角的角.
图中包含了( )个小于平角的角.| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
13.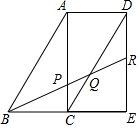 取三个完全相同的三角板拼成如图所示的形状,R为DE的中点,BR分别交AC,CD于P,Q,则BP:PQ:QR=( )
取三个完全相同的三角板拼成如图所示的形状,R为DE的中点,BR分别交AC,CD于P,Q,则BP:PQ:QR=( )
 取三个完全相同的三角板拼成如图所示的形状,R为DE的中点,BR分别交AC,CD于P,Q,则BP:PQ:QR=( )
取三个完全相同的三角板拼成如图所示的形状,R为DE的中点,BR分别交AC,CD于P,Q,则BP:PQ:QR=( )| A. | 3:1:2 | B. | 5:2:3 | C. | 4:1:3 | D. | 6:1:3 |
18. 如图,正六边形ABCDEF内接于⊙O,连结AC,EB,CH=6$\sqrt{3}$,则EH的长为( )
如图,正六边形ABCDEF内接于⊙O,连结AC,EB,CH=6$\sqrt{3}$,则EH的长为( )
 如图,正六边形ABCDEF内接于⊙O,连结AC,EB,CH=6$\sqrt{3}$,则EH的长为( )
如图,正六边形ABCDEF内接于⊙O,连结AC,EB,CH=6$\sqrt{3}$,则EH的长为( )| A. | 12$\sqrt{3}$ | B. | 18 | C. | 6$\sqrt{3}$+6 | D. | 12 |