题目内容
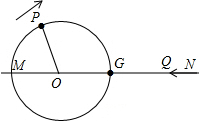
19．解答题（1）如图1，线段MN=30cm，MO=GO=3cm，点P从点M开始绕着点O以15°/s的速度顺时针旋转一周回到点M后停止，点Q同时出发沿射线NM自N点向M点运动，若点P、Q两点能恰好相遇，则点Q运动的速度为1.25或2cm/s．
（2）要使（x2+mx+8）（x2-3x+n）的展开式中不含x3项和x2项，求m，n的值．
分析 （1）由于点P，Q只能在直线AB上相遇，而点P旋转到直线AB上的时间分两种情况，所以根据题意列出方程分别求解；
（2）原式利用多项式乘以多项式法则计算得到结果，由结果不含x3项和x2项，求出m与n的值即可．
解答 解：（1）∵点P在⊙O上绕点O旋转的速度为15°/s，
∴点P到达点G的时间为180°÷15°=12s，
回到点M的时间为360°÷15°=24s，
设点Q的速度为xcm/s，
则有12x=30-3×2，解得x=2；
或24x=30，解得x=1.25．
答：点Q的速度为2cm/s或1.25cm/s．
故答案为：1.25或2；
（2）（x2+mx+8）（x2-3x+n）=x4-3x3+nx2+mx3-3mx2+mnx+8x2-24x+8n=x4+（m-3）x3+（n-3m+8）x2+（mn-24）x+8n，
由结果不含x3项和x2项，得到m-3=0，n-3m+8=0，
解得：m=3，n=1．
点评 此题考查的是一元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程，再求解．也考查了多项式乘多项式．
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
13．
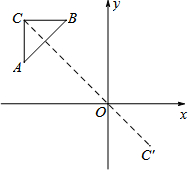如图，△ABC的顶点坐标分别为A（-4，2），B（-2，4），C（-4，4），以原点O为位似中心，将△ABC缩小后得到△A′B′C′．若点C的对应点C′的坐标为（2，-2），则点A的对应点A′的坐标为（ ）
如图，△ABC的顶点坐标分别为A（-4，2），B（-2，4），C（-4，4），以原点O为位似中心，将△ABC缩小后得到△A′B′C′．若点C的对应点C′的坐标为（2，-2），则点A的对应点A′的坐标为（ ）| A． | （2，-3） | B． | （2，-1） | C． | （3，-2） | D． | （1，-2） |
10．
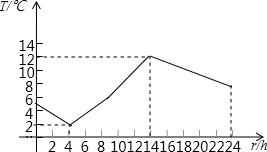如图是自动温度计记录的某一天气温变化的曲线，它反映了变量T（℃）与t（h）之间的对应关系，这一天中，温差（最高与最低温度的差）是（ ）
如图是自动温度计记录的某一天气温变化的曲线，它反映了变量T（℃）与t（h）之间的对应关系，这一天中，温差（最高与最低温度的差）是（ ）| A． | 10℃ | B． | -10℃ | C． | 8℃ | D． | 12℃ |
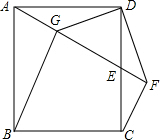如图，已知在正方形ABCD中，点E在CD边长，过C点作AE的垂线交于点F，联结DF，过点D作DF的垂线交A于点G，联结BG．