题目内容
6.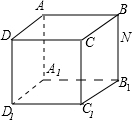 如图是一个棱长为4cm的正方体盒子,且蚂蚁在正方体盒子的内部D1C1的中点M处.它爬到BB1的中点N的最短路线长是2$\sqrt{10}$cm.
如图是一个棱长为4cm的正方体盒子,且蚂蚁在正方体盒子的内部D1C1的中点M处.它爬到BB1的中点N的最短路线长是2$\sqrt{10}$cm.
分析 把此正方体的DCC1D1面与CC1B1B面展开在同一平面内,然后利用勾股定理求点M和N点间的线段长,即可得到蚂蚁爬行的最短距离.在直角三角形MNB1中,一条直角边长等于6,另一条直角边长等于2,利用勾股定理可得出结论.
解答  解:如图所示,
解:如图所示,
MN=$\sqrt{{2}^{2}+(2+6)^{2}}$=2$\sqrt{10}$(cm).
故答案为:2$\sqrt{10}$cm.
点评 本题考查了的是平面展开-最短路径问题,“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
14. 如图,AD、BE是△ABC的中线,则下列结论中,正确的个数有( )
如图,AD、BE是△ABC的中线,则下列结论中,正确的个数有( )
(1)S△AOE=S△COE; (2)S△AOB=S四边形EODC;
(3)S△BOC=2S△COE; (4)S△ABC=4S△BOC.
 如图,AD、BE是△ABC的中线,则下列结论中,正确的个数有( )
如图,AD、BE是△ABC的中线,则下列结论中,正确的个数有( )(1)S△AOE=S△COE; (2)S△AOB=S四边形EODC;
(3)S△BOC=2S△COE; (4)S△ABC=4S△BOC.
| A. | .1个 | B. | .2个 | C. | .3个 | D. | .4个 |
11.3月15日是国际消费者权益日.某品牌专卖店准备出售甲、乙两种服装.其中甲、乙两种服装的进价和售价如表:
已知:专卖店用3000元购进甲种服装的数量与用2400元购进乙种服装的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种服装共200件的总利润(利润=售价-进价)不少于21700元,且甲种服装的件数不超过总件数的一半,问该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备对甲种服装进行优惠促销活动,决定对甲种服装每件优惠a(50<a<70)元出售,乙种服装价格不变.那么该专卖店要获得最大利润应如何进货?
| 服装价格 | 甲 | 乙 |
| 进价(元/件) | m | m-20 |
| 售价(元/件) | 240 | 160 |
(1)求m的值;
(2)要使购进的甲、乙两种服装共200件的总利润(利润=售价-进价)不少于21700元,且甲种服装的件数不超过总件数的一半,问该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备对甲种服装进行优惠促销活动,决定对甲种服装每件优惠a(50<a<70)元出售,乙种服装价格不变.那么该专卖店要获得最大利润应如何进货?
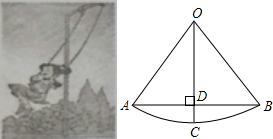 如图,小丽荡秋千,秋千链子的长OA为2.5米,秋千向两边摆动的角度相同,摆动的水平距离AB为3米,则秋千摆至最高位置时与最低价位置时的高度之差(即CD)为0.5米.
如图,小丽荡秋千,秋千链子的长OA为2.5米,秋千向两边摆动的角度相同,摆动的水平距离AB为3米,则秋千摆至最高位置时与最低价位置时的高度之差(即CD)为0.5米.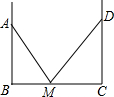 如图,装修师傅装修一间房子,在两墙之间有一个底端在点M的梯子,当它靠在一侧墙上时,梯子的顶端在点A,当它靠在另一侧墙上时,梯子的顶端在点D,已知∠AMB=55°,∠DMC=44°,点A到地面的垂直距离为4m,求点D到地面垂直的距离.(参考数据:sin55°≈0.8192,sin44°≈0.6947)
如图,装修师傅装修一间房子,在两墙之间有一个底端在点M的梯子,当它靠在一侧墙上时,梯子的顶端在点A,当它靠在另一侧墙上时,梯子的顶端在点D,已知∠AMB=55°,∠DMC=44°,点A到地面的垂直距离为4m,求点D到地面垂直的距离.(参考数据:sin55°≈0.8192,sin44°≈0.6947)