题目内容
19.若a+b=6,ab=2,则$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=8.分析 首先把分式进行通分,可得$\frac{{b}^{2}+{a}^{2}}{{a}^{2}{b}^{2}}$,再根据完全平方公式可得$\frac{(a+b)^{2}-2ab}{(ab)^{2}}$,然后再代入a+b=6,ab=2可得答案.
解答 解:$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$
=$\frac{{b}^{2}+{a}^{2}}{{a}^{2}{b}^{2}}$
=$\frac{(a+b)^{2}-2ab}{(ab)^{2}}$
=$\frac{36-4}{4}$
=8.
故答案为:8.
点评 此题主要考查了分式的化简求值,关键是掌握分式的通分和完全平方公式.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
7.直线y=2x+3经过点(2,m),则m的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 7 | D. | -7 |
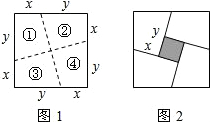 如图1,将正方形沿图中虚线(其中x<y)剪成①②③④四块图形,用这四块图形恰好能拼成一个四边形.
如图1,将正方形沿图中虚线(其中x<y)剪成①②③④四块图形,用这四块图形恰好能拼成一个四边形. 如图,网格中的每一格的边长为1个单位长度,已知四边形ABCD的顶点均在网格的个点上.
如图,网格中的每一格的边长为1个单位长度,已知四边形ABCD的顶点均在网格的个点上. (1)计算:|1-$\sqrt{2}$|+$\root{3}{-\frac{8}{27}}$×$\sqrt{\frac{1}{4}}$-$\sqrt{2}$
(1)计算:|1-$\sqrt{2}$|+$\root{3}{-\frac{8}{27}}$×$\sqrt{\frac{1}{4}}$-$\sqrt{2}$