题目内容
9. (1)计算:|1-$\sqrt{2}$|+$\root{3}{-\frac{8}{27}}$×$\sqrt{\frac{1}{4}}$-$\sqrt{2}$
(1)计算:|1-$\sqrt{2}$|+$\root{3}{-\frac{8}{27}}$×$\sqrt{\frac{1}{4}}$-$\sqrt{2}$(2)解方程组:$\left\{\begin{array}{l}{8x+9y=12①}\\{x-3y=18②}\end{array}\right.$
(3)解不等式组$\left\{\begin{array}{l}{2-x>0①}\\{\frac{5x+1}{2}+1≥\frac{2x-1}{3}②}\end{array}\right.$并把它的解集表示在如图数轴上.
分析 (1)根据实数的运算方法,首先计算开方和乘法,然后从左向右依次计算,求出算式的值是多少即可.
(2)应用代入法解二元一次方程组,求出方程组的解是多少即可.
(3)首先根据解一元一次不等式组的方法,求出不等式组的解集是多少;然后把不等式组的解集表示在数轴上即可.
解答 解:(1)|1-$\sqrt{2}$|+$\root{3}{-\frac{8}{27}}$×$\sqrt{\frac{1}{4}}$-$\sqrt{2}$
=$\sqrt{2}-1$+($-\frac{2}{3}$)×$\frac{1}{2}$$-\sqrt{2}$
=$\sqrt{2}-1-\frac{1}{3}-\sqrt{2}$
=-$\frac{4}{3}$
(2)由②,可得:x=3y+18,
把x=3y+18代入①,可得
8(3y+18)+9y=12,
解得y=-4,
把y=-4代入x=3y+18,可得
x=3×(-4)+18=6,
∴方程组$\left\{\begin{array}{l}{8x+9y=12①}\\{x-3y=18②}\end{array}\right.$的解为:
$\left\{\begin{array}{l}{x=6}\\{y=-4}\end{array}\right.$.
(3)解不等式①,可得:x<2,
解不等式②,可得:x≥-1,
∴不等式组的解集是:-1≤x<2,
把它的解集表示在数轴上为: .
.
点评 (1)此题主要考查了实数的四则混合运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到有的顺序进行.另外,有理数的运算律在实数范围内仍然适用.
(2)此题还考查了解一元一次不等式组的方法,以及在数轴上表示不等式的解集的方法,要熟练掌握.
(3)此题还考查了解二元一次方程组的方法,要熟练掌握两种常用的方法:代入法和消元法.

| A. | “抛掷一枚硬币,硬币落地时正面朝上”是随机事件 | |
| B. | “任意打开数学教科书八年级下册,正好是第50页”是不可能事件 | |
| C. | “把4个球放入三个抽屉中,其中必有一个抽屉中至少有2个球”是必然事件 | |
| D. | “在一个不透明的袋子中,有5个除颜色外完全一样的小球,其中2个红球,3个白球,从中任意摸出1个小球,正好是红球”是随机事件 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,从A到B的四条路径中,最短的路线是( )
如图,从A到B的四条路径中,最短的路线是( )| A. | A-E-G-B | B. | A-E-C-B | C. | A-E-G-D-B | D. | A-E-F-B |
| A. | -6 | B. | -9 | C. | ±6 | D. | ±9 |
 如图,把△ABC绕点C按逆时针方向旋转35°得到△A′B′C,A′B′交BC于点D,若∠A′DC=90°,则∠B=55°.
如图,把△ABC绕点C按逆时针方向旋转35°得到△A′B′C,A′B′交BC于点D,若∠A′DC=90°,则∠B=55°.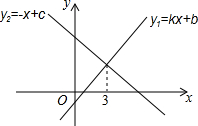 一次函数y1=kx+b与y2=-x+c的图象如图,则kx+b≥-x+c的解集是x>3.
一次函数y1=kx+b与y2=-x+c的图象如图,则kx+b≥-x+c的解集是x>3.