题目内容
在△ABC中,AB=AC=10,cosB=
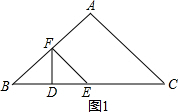
(如图1),D、E为线段BC上的两个动点,且DE=3(E在D右边),运动初始时D和B重合,运动至E和C重合时运动终止.过E作EF∥AC交AB于F,联结DF.
(1)若设BD=x,EF=y,求y关于x的函数,并求其定义域;
(2)如果△BDF为直角三角形,求△BDF的面积;
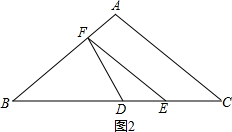
(3)如果MN过△DEF的重心,且MN∥BC分别交FD、FE于M、N(如图2).求整个运动过程中线段MN扫过的区域的形状和面积(直接写出答案).

| 4 |
| 5 |
(1)若设BD=x,EF=y,求y关于x的函数,并求其定义域;
(2)如果△BDF为直角三角形,求△BDF的面积;
(3)如果MN过△DEF的重心,且MN∥BC分别交FD、FE于M、N(如图2).求整个运动过程中线段MN扫过的区域的形状和面积(直接写出答案).

考点:相似形综合题
专题:
分析:(1)根据三角形ABC为等腰三角形,腰AB=AC=10,底角B满足cosB=
,可求得BC,再由EF∥AC,则
=
,把BD=x,EF=y,DE=3代入即可得出
y关于x的函数,再写出再写出自变量的取值范围即可,(0≤x≤13).
(2)依题意易得出FB=FE=
(x+3).若∠FDB为直角时有BD=DE.可得出x的值为3,根据cosB=
,得FD,从而得出三角形BDF的面积;若∠BFD为直角时,则BF=EF即可得出x的值,从而得出三角形BDF的面积;
(3)根据MN∥BC,可得出线段MN扫过的区域的形状是平行四边形,直接写出面积即可.
| 4 |
| 5 |
| EF |
| AC |
| BE |
| BC |
y关于x的函数,再写出再写出自变量的取值范围即可,(0≤x≤13).
(2)依题意易得出FB=FE=
| 5 |
| 8 |
| 4 |
| 5 |
(3)根据MN∥BC,可得出线段MN扫过的区域的形状是平行四边形,直接写出面积即可.
解答:解:(1)∵在等腰三角形ABC中,腰AB=AC=10,底角B满足cosB=
,
∴BC=10×
×2=16.
∵EF∥AC,
∴
=
.
BD=x,EF=y,DE=3
∴y=
(x+3).(0≤x≤13).
(2)依题意易得在三角形FBE中,FB=FE=
(x+3).
若∠FDB为直角时(如图1),有BD=DE.
∴x=3
又∵cosB=
,
 ∴FD=
∴FD=
BD=
×3=
.
∴三角形BDF的面积为
×
×3
.
若∠BFD为直角时(如图2),BF=EF=
(x+3)=
,
∴x=
,
∴△BDF的面积为
×
×
×
×
=
,
(3)平行四边形.面积为
.
| 4 |
| 5 |
∴BC=10×
| 4 |
| 5 |
∵EF∥AC,
∴
| EF |
| AC |
| BE |
| BC |
BD=x,EF=y,DE=3
∴y=
| 5 |
| 8 |

(2)依题意易得在三角形FBE中,FB=FE=
| 5 |
| 8 |
若∠FDB为直角时(如图1),有BD=DE.
∴x=3
又∵cosB=
| 4 |
| 5 |
 ∴FD=
∴FD=| 3 |
| 4 |
| 3 |
| 4 |
| 9 |
| 4 |
∴三角形BDF的面积为
| 1 |
| 2 |
| 9 |
| 4 |
| 27 |
| 8 |
若∠BFD为直角时(如图2),BF=EF=
| 5 |
| 8 |
| 4x |
| 5 |
∴x=
| 75 |
| 7 |
∴△BDF的面积为
| 1 |
| 2 |
| 75 |
| 7 |
| 4 |
| 5 |
| 75 |
| 7 |
| 3 |
| 5 |
| 1350 |
| 49 |
(3)平行四边形.面积为
| 13 |
| 4 |
点评:本题考查了相似三角形的综合运用,以及三角函数、勾股定理和三角形面积的计算,本题是难度较大的动点题目,在做题时要认真思考每一个已知条件,是解决问题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
 如图,游客从某旅游景区的景点A处下山至C处有两种路径,一中是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客同时从A处下山,甲沿AC匀速步行,速度为45m/min.乙开始从A乘缆车到B,在B处停留5min后,再从B匀速步行到C,两人同时到达.已知缆车匀速直线运动的速度为180m/min,山路AC长为2430m,经测量,∠CAB=45°,∠CBA=105°.(参考数据:
如图,游客从某旅游景区的景点A处下山至C处有两种路径,一中是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客同时从A处下山,甲沿AC匀速步行,速度为45m/min.乙开始从A乘缆车到B,在B处停留5min后,再从B匀速步行到C,两人同时到达.已知缆车匀速直线运动的速度为180m/min,山路AC长为2430m,经测量,∠CAB=45°,∠CBA=105°.(参考数据: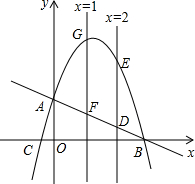 如图,抛物线与x轴相交于B、C两点,与y轴相交于点A,P(a,-a2+
如图,抛物线与x轴相交于B、C两点,与y轴相交于点A,P(a,-a2+ 如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).
如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).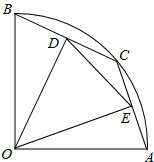 【倾听理解】(这是习题讲评课上师生围绕一道习题的对话片断)
【倾听理解】(这是习题讲评课上师生围绕一道习题的对话片断)
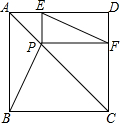 如图,已知P是正方形ABCD对角线AC上的一点,不与A,C重合,PE⊥DA,PF⊥CD,E、F为垂足,
如图,已知P是正方形ABCD对角线AC上的一点,不与A,C重合,PE⊥DA,PF⊥CD,E、F为垂足, 如图,已知AD是∠BAC的平分线,在不添加任何辅助线的前提下,要使△AED≌△AFD,还需添加一个条件,这个条件可以是
如图,已知AD是∠BAC的平分线,在不添加任何辅助线的前提下,要使△AED≌△AFD,还需添加一个条件,这个条件可以是