题目内容
 如图,在平面直角坐标系中,矩形OABC的对角线AC=10,cos∠OCA=
如图,在平面直角坐标系中,矩形OABC的对角线AC=10,cos∠OCA=| 3 |
| 5 |
(1)求点A的坐标;
(2)求直线MN的解析式;
(3)若反比例函数y=
| k |
| x |
考点:一次函数综合题
专题:综合题
分析:(1)在直角三角形ACO中,由AC与cos∠OCA,利用锐角三角函数定义求出OC的长,再利用勾股定理求出OA的长,即可确定出A的坐标;
(2)MN是矩形OABC对折后折痕所在的直线,即MN为AC的中垂线,设MN与AC的交点为P,则有PA=PC=5,利用锐角三角函数定义求出AN的长,进而求出ON的长,确定出N点坐标,同理求出CM的长,确定出M点坐标,设直线MN解析式为y=kx+b,将M与N坐标代入求出k与b的值,即可确定出直线MN解析式;
(3)设直线AC解析式为y=ax+m,将A与C坐标代入求出a与m的值,确定出直线AC解析式,与反比例函数解析式联立,消元y得到关于x的一元二次方程,根据反比例函数与线段AC有公共点,得到根的判别式大于等于0,即可确定出k的范围.
(2)MN是矩形OABC对折后折痕所在的直线,即MN为AC的中垂线,设MN与AC的交点为P,则有PA=PC=5,利用锐角三角函数定义求出AN的长,进而求出ON的长,确定出N点坐标,同理求出CM的长,确定出M点坐标,设直线MN解析式为y=kx+b,将M与N坐标代入求出k与b的值,即可确定出直线MN解析式;
(3)设直线AC解析式为y=ax+m,将A与C坐标代入求出a与m的值,确定出直线AC解析式,与反比例函数解析式联立,消元y得到关于x的一元二次方程,根据反比例函数与线段AC有公共点,得到根的判别式大于等于0,即可确定出k的范围.
解答: 解:(1)在Rt△ACO中,∵AC=10,cos∠OCA=
解:(1)在Rt△ACO中,∵AC=10,cos∠OCA=
,
∴cos∠OCA=
=
,即
=
,
∴OC=6,
∴OA=
=
=8,
∴点A的坐标为 (8,0);
(2)MN是矩形OABC对折后折痕所在的直线,即MN为AC的中垂线,
设MN与AC的交点为P,则有PA=PC=
AC=5,
∴cos∠CAO=
=
,即
=
,
∴AN=
,ON=OA-AN=8-
=
.
∴N(
,0),
同理CM=AN=0A-ON=8-
=
,
∴M(
,6),
设直线MN的解析式为y=kx+b,
∴
,
解得:
,
则直线MN解析式为y=
x-
;
(3)设直线AC解析式为y=ax+m,
将A(8,0),C(0,6)代入得:
,
解得:a=-
,m=6,
∴线段AC解析式为y=-
x+6(0≤x≤8),
联立得:
,
消去y得:-
x+6=
,
整理得:3x2-24x+4k=0,
∵反比例函数与线段AC有公共点,
∴△=242-4×3×4k≥0,
解得:k≤12,
∵反比例函数在x>0时,图象位于第一象限,
∴k>0,
则k的范围为0<k≤12.
 解:(1)在Rt△ACO中,∵AC=10,cos∠OCA=
解:(1)在Rt△ACO中,∵AC=10,cos∠OCA=| 3 |
| 5 |
∴cos∠OCA=
| OC |
| AC |
| 3 |
| 5 |
| OC |
| 10 |
| 3 |
| 5 |
∴OC=6,
∴OA=
| AC2-OC2 |
| 102-62 |
∴点A的坐标为 (8,0);
(2)MN是矩形OABC对折后折痕所在的直线,即MN为AC的中垂线,
设MN与AC的交点为P,则有PA=PC=
| 1 |
| 2 |
∴cos∠CAO=
| OA |
| AC |
| AP |
| AN |
| 8 |
| 10 |
| 5 |
| AN |
∴AN=
| 25 |
| 4 |
| 25 |
| 4 |
| 7 |
| 4 |
∴N(
| 7 |
| 4 |
同理CM=AN=0A-ON=8-
| 7 |
| 4 |
| 25 |
| 4 |
∴M(
| 25 |
| 4 |
设直线MN的解析式为y=kx+b,
∴
|
解得:
|
则直线MN解析式为y=
| 4 |
| 3 |
| 7 |
| 3 |
(3)设直线AC解析式为y=ax+m,
将A(8,0),C(0,6)代入得:
|
解得:a=-
| 3 |
| 4 |
∴线段AC解析式为y=-
| 3 |
| 4 |
联立得:
|
消去y得:-
| 3 |
| 4 |
| k |
| x |
整理得:3x2-24x+4k=0,
∵反比例函数与线段AC有公共点,
∴△=242-4×3×4k≥0,
解得:k≤12,
∵反比例函数在x>0时,图象位于第一象限,
∴k>0,
则k的范围为0<k≤12.
点评:此题属于一次函数综合题,涉及的知识有:待定系数法求函数解析式,一次函数与反比例函数的交点,坐标与图形性质,锐角三角函数定义,勾股定理,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目

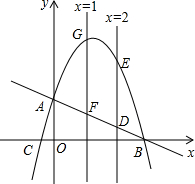 如图,抛物线与x轴相交于B、C两点,与y轴相交于点A,P(a,-a2+
如图,抛物线与x轴相交于B、C两点,与y轴相交于点A,P(a,-a2+ 如图,已知△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90° 请你在图中找出一对全等的三角形,并证明你的结论.
如图,已知△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90° 请你在图中找出一对全等的三角形,并证明你的结论.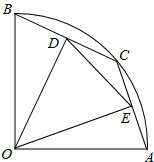 【倾听理解】(这是习题讲评课上师生围绕一道习题的对话片断)
【倾听理解】(这是习题讲评课上师生围绕一道习题的对话片断)
 某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为67°,在教学楼三楼D处测得旗杆顶部的仰角为37°,旗杆底部与教学楼一楼在同一水平线上,已知每层的高度为3m,求旗杆AB的高度(精确到0.1m).(参考数据:tan67°≈
某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为67°,在教学楼三楼D处测得旗杆顶部的仰角为37°,旗杆底部与教学楼一楼在同一水平线上,已知每层的高度为3m,求旗杆AB的高度(精确到0.1m).(参考数据:tan67°≈ 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,直角∠MON的顶点O在AB上,OM、ON分别交CA、CB于点P、Q,∠MON绕点O任意旋转.当
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,直角∠MON的顶点O在AB上,OM、ON分别交CA、CB于点P、Q,∠MON绕点O任意旋转.当