题目内容
阅读下面文字,解决下列问题
(1)问题背景 宇昕同学遇到这样一个问题:如图1,在正方形ABCD中,点E,F分别为BC,CD上的点,且∠EAF=45°,求证:BE+DF=EF.
宇昕是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段集中到同一条线段上.他先后尝试了平移、翻折、旋转的方法,发现通过旋转可以解决此问题.
他的方法是将△ADF绕点A顺时针旋转90°得到△ABG(如图2),此时GE即是DF+BE.
请回答:在图2中,∠GAF的度数是 、△AGE≌△ .
(2)拓展研究 如图3,若E,F分别在四边形ABCD的边BC,CD上,∠B+∠D=180°,AB=AD,要使(1)中线段BE,EF,FD的等量关系仍然成立,则∠EAF与∠BAD应满足的关系是 .
(3)构造运用 运用(1)(2)解答中所积累的经验和知识,完成下面问题:如图4,在四边形ABCD中,∠ABC=90°,∠CAB=∠CAD=22.5°,点E在AB上,且∠DCE=67.5°,DE⊥AB于点E,若AE=3
,试求线段AD,BE的长.

(1)问题背景 宇昕同学遇到这样一个问题:如图1,在正方形ABCD中,点E,F分别为BC,CD上的点,且∠EAF=45°,求证:BE+DF=EF.
宇昕是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段集中到同一条线段上.他先后尝试了平移、翻折、旋转的方法,发现通过旋转可以解决此问题.
他的方法是将△ADF绕点A顺时针旋转90°得到△ABG(如图2),此时GE即是DF+BE.
请回答:在图2中,∠GAF的度数是
(2)拓展研究 如图3,若E,F分别在四边形ABCD的边BC,CD上,∠B+∠D=180°,AB=AD,要使(1)中线段BE,EF,FD的等量关系仍然成立,则∠EAF与∠BAD应满足的关系是
(3)构造运用 运用(1)(2)解答中所积累的经验和知识,完成下面问题:如图4,在四边形ABCD中,∠ABC=90°,∠CAB=∠CAD=22.5°,点E在AB上,且∠DCE=67.5°,DE⊥AB于点E,若AE=3
| 2 |

考点:全等三角形的判定与性质,正方形的性质,旋转的性质
专题:
分析:(1)将△ADF绕点A顺时针旋转90°得到△ABG,所以AG=AF,∠GAF=90°因为∠EAF=45°,所以∠GAE=∠EAF=45°,从而证得△AGE≌△AEF;
(2)延长FD使DG=BE,连接AG,可证得△ABE≌△ADG,从而证得△AEF≌△AFG,则可证得∠EAF=
∠BAD;
(3)由∠CAB=∠CAD=22.5°可得∠DAE=45°,DE⊥AB所以DE=AE=3
.根据勾股定理可求得AD=6,由∠CAB=∠CAD=22.5°根据角的平分线上的点到两边的点到两边的距离相等,可证得BC=CF,然后证得△CBG≌△CFD,再证得△CGE≌△CED,求得∠3=∠4=45°,从而求得CE=AE=3
,在△CBE中根据勾股定理求得BE的长,
(2)延长FD使DG=BE,连接AG,可证得△ABE≌△ADG,从而证得△AEF≌△AFG,则可证得∠EAF=
| 1 |
| 2 |
(3)由∠CAB=∠CAD=22.5°可得∠DAE=45°,DE⊥AB所以DE=AE=3
| 2 |
| 2 |
解答:解;(1)∠GAF的度数是 90°、△AGE≌△AEF;
将△ADF绕点A顺时针旋转90°得到△ABG,
∠GAB=∠DAF,GB=DF,
∵∠GAF=90°,∠EAF=45°;
∴∠GAE=∠EAF=45°;
在△AGE与△AEF中
∴
,
∴△AGE≌△AEF(SAS),
∴GB+BE=EF,
∵GB=DF,
∴BE+DF=EF.

(2)∠EAF=
∠BAD,
延长FD使DG=BE,连接AG
∵∠B+∠ADC=180°,∠ADG+∠ADC=180°
∴∠B=∠ADG;
在△ABE于△ADG中
∴△ABE≌△ADG(SAS)
∴∠BAE=∠DAG,AE=AG;
∵BE+DF=EF,DG=BE,
∴DG+DF=EF,
即GF=EF,
在△AEF与△AFG中
∴△AEF≌△AFG(SSS),
∴∠FAG=∠EAF,
∵∠BAE=∠DAG,
∴∠BAE+∠CAD=∠FAG,
∴∠EAF=
∠BAD.
(3)∵∠CAB=∠CAD=22.5°,
∴∠DAE=45°,
又∵∠AED=90°,
∴DE=AE=3
,
∴AD=
=6.
延长AD,过点C作CF垂直AD于F,
由∠CAB=∠CAD可知AC为∠BAD的角平分线,
∴CB=CF,
把三角形CDF绕点C旋转到CF与CB重合,则DF与GB重合.
∴CG=CD,∠GCB=∠DCF;
∵CB⊥AB,CF⊥AD,∠CAB=∠CAD=22.5°;
∴∠ACB=∠ACF=67.5°=∠DCE
∴∠DCA=∠2=∠3,∠DCA+∠DCF=∠2+∠GCB=∠DCE=67.5°,
在△DCE与△GCE中
,
∴△DCE≌△GCE(SAS),
∴∠3=∠4=45°,
∵∠CAB=∠CAD=22.5°,∠4=∠CAB+∠ACE,
∴∠ACE=∠CAB=22.5°,
∴CE=AE=3
,
在Rt△CBE中,BE2+BC2=CE2,
即BE=
=3.

将△ADF绕点A顺时针旋转90°得到△ABG,
∠GAB=∠DAF,GB=DF,
∵∠GAF=90°,∠EAF=45°;
∴∠GAE=∠EAF=45°;
在△AGE与△AEF中
∴
|
∴△AGE≌△AEF(SAS),
∴GB+BE=EF,
∵GB=DF,
∴BE+DF=EF.

(2)∠EAF=
| 1 |
| 2 |
延长FD使DG=BE,连接AG
∵∠B+∠ADC=180°,∠ADG+∠ADC=180°
∴∠B=∠ADG;
在△ABE于△ADG中
|
∴△ABE≌△ADG(SAS)
∴∠BAE=∠DAG,AE=AG;
∵BE+DF=EF,DG=BE,
∴DG+DF=EF,
即GF=EF,
在△AEF与△AFG中
|
∴△AEF≌△AFG(SSS),
∴∠FAG=∠EAF,
∵∠BAE=∠DAG,
∴∠BAE+∠CAD=∠FAG,
∴∠EAF=
| 1 |
| 2 |
(3)∵∠CAB=∠CAD=22.5°,
∴∠DAE=45°,
又∵∠AED=90°,
∴DE=AE=3
| 2 |
∴AD=
| DE2+AE2 |
延长AD,过点C作CF垂直AD于F,
由∠CAB=∠CAD可知AC为∠BAD的角平分线,
∴CB=CF,
把三角形CDF绕点C旋转到CF与CB重合,则DF与GB重合.
∴CG=CD,∠GCB=∠DCF;
∵CB⊥AB,CF⊥AD,∠CAB=∠CAD=22.5°;
∴∠ACB=∠ACF=67.5°=∠DCE
∴∠DCA=∠2=∠3,∠DCA+∠DCF=∠2+∠GCB=∠DCE=67.5°,
在△DCE与△GCE中
|
∴△DCE≌△GCE(SAS),
∴∠3=∠4=45°,
∵∠CAB=∠CAD=22.5°,∠4=∠CAB+∠ACE,
∴∠ACE=∠CAB=22.5°,
∴CE=AE=3
| 2 |
在Rt△CBE中,BE2+BC2=CE2,
即BE=
|

点评:本题主要考查了全等三角形的判定和性质,勾股定理的应用,角平分线的性质,此题是开放性试题,首先在特殊图形中找到规律,然后再推广到一般图形中,对学生的分析问题,解决问题的能力要求比较高.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
比0大的数是( )
| A、-2 | ||
B、-
| ||
| C、0 | ||
| D、0.001 |
 如图,已知点G是梯形ABCD的中位线EF上任意一点,若梯形ABCD的面积为24cm2,则图中阴影部分的面积为
如图,已知点G是梯形ABCD的中位线EF上任意一点,若梯形ABCD的面积为24cm2,则图中阴影部分的面积为
 如图,游客从某旅游景区的景点A处下山至C处有两种路径,一中是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客同时从A处下山,甲沿AC匀速步行,速度为45m/min.乙开始从A乘缆车到B,在B处停留5min后,再从B匀速步行到C,两人同时到达.已知缆车匀速直线运动的速度为180m/min,山路AC长为2430m,经测量,∠CAB=45°,∠CBA=105°.(参考数据:
如图,游客从某旅游景区的景点A处下山至C处有两种路径,一中是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客同时从A处下山,甲沿AC匀速步行,速度为45m/min.乙开始从A乘缆车到B,在B处停留5min后,再从B匀速步行到C,两人同时到达.已知缆车匀速直线运动的速度为180m/min,山路AC长为2430m,经测量,∠CAB=45°,∠CBA=105°.(参考数据: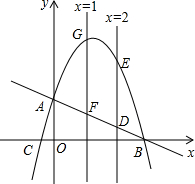 如图,抛物线与x轴相交于B、C两点,与y轴相交于点A,P(a,-a2+
如图,抛物线与x轴相交于B、C两点,与y轴相交于点A,P(a,-a2+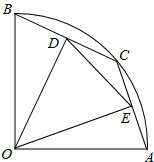 【倾听理解】(这是习题讲评课上师生围绕一道习题的对话片断)
【倾听理解】(这是习题讲评课上师生围绕一道习题的对话片断)
 如图,在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧
如图,在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧