题目内容
18.已知点M(1,m2+1)在双曲线y=$\frac{k}{x}$上,则双曲线y=$\frac{k}{x}$一定分布在( )象限.| A. | 一、二 | B. | 一、三 | C. | 二、三 | D. | 二、四 |
分析 根据图象上的点(x,y)的横纵坐标的积是定值k,即xy=k可得k=m2+1>0,再根据当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小可得答案.
解答 解:∵点M(1,m2+1)在双曲线y=$\frac{k}{x}$上,
∴k=1•(m2+1)=>0,
∴双曲线y=$\frac{k}{x}$一定分布在第一、三象限,
故选:B.
点评 此题主要考查了反比例函数的性质和反比例函数图象上点的坐标特点,关键是掌握反比例函数图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.若x,y为实数,且|x+2|+$\sqrt{y-2}$=0,则$\frac{x}{y}$的值为( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
9.正方形具有而矩形不一定具有的性质是( )
| A. | 对角线相等 | B. | 对角线互相平分 | ||
| C. | 对角线互相垂直 | D. | 对角线互相平分且相等 |
6.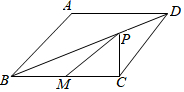 如图,菱形ABCD的边长为4cm,∠ABC=60°,且M为BC的中点,P是对角线BD上的一动点,则PM+PC的最小值为( )
如图,菱形ABCD的边长为4cm,∠ABC=60°,且M为BC的中点,P是对角线BD上的一动点,则PM+PC的最小值为( )
 如图,菱形ABCD的边长为4cm,∠ABC=60°,且M为BC的中点,P是对角线BD上的一动点,则PM+PC的最小值为( )
如图,菱形ABCD的边长为4cm,∠ABC=60°,且M为BC的中点,P是对角线BD上的一动点,则PM+PC的最小值为( )| A. | 4 cm | B. | $\sqrt{3}$cm | C. | 2$\sqrt{5}$cm | D. | 2$\sqrt{3}$cm |
13.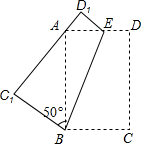 如图,将一个矩形纸片ABCD,沿着BE折叠,使C、D两点分别落在点C1、D1处.若∠C1BA=50°,则∠ABE的度数为( )
如图,将一个矩形纸片ABCD,沿着BE折叠,使C、D两点分别落在点C1、D1处.若∠C1BA=50°,则∠ABE的度数为( )
 如图,将一个矩形纸片ABCD,沿着BE折叠,使C、D两点分别落在点C1、D1处.若∠C1BA=50°,则∠ABE的度数为( )
如图,将一个矩形纸片ABCD,沿着BE折叠,使C、D两点分别落在点C1、D1处.若∠C1BA=50°,则∠ABE的度数为( )| A. | 10° | B. | 20° | C. | 30° | D. | 40° |
3.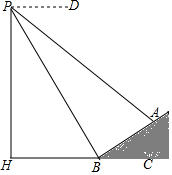 如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°,已知tan∠ABC=$\frac{\sqrt{3}}{3}$,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥BC,则A,B两点间的距离为( )米.
如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°,已知tan∠ABC=$\frac{\sqrt{3}}{3}$,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥BC,则A,B两点间的距离为( )米.
 如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°,已知tan∠ABC=$\frac{\sqrt{3}}{3}$,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥BC,则A,B两点间的距离为( )米.
如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°,已知tan∠ABC=$\frac{\sqrt{3}}{3}$,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥BC,则A,B两点间的距离为( )米.| A. | 200$\sqrt{3}$ | B. | 200 | C. | 100$\sqrt{3}$ | D. | 100 |
5.下列图形具有稳定性的是( )
| A. | 正五边形 | B. | 三角形 | C. | 梯形 | D. | 正方形 |
 四个相同的小正方体搭建了一个积木,它的左视图和主视图均如图所示,则这堆积木不可能是( )
四个相同的小正方体搭建了一个积木,它的左视图和主视图均如图所示,则这堆积木不可能是( )



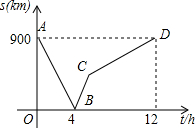 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为t(h),两车之间的距离为s(km),图中的折线表示s与t之间的函数关系,根据图象提供的信息有下列说法:①甲、乙两地之间的距离为900km; ②行驶4h两车相遇; ③快车的速度为150km/h; ④行驶6h两车相距450km; ⑤相遇时慢车行驶了280km; ⑥行驶6h快车停止了行驶.其中符合图象描述的说法有( )个.
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为t(h),两车之间的距离为s(km),图中的折线表示s与t之间的函数关系,根据图象提供的信息有下列说法:①甲、乙两地之间的距离为900km; ②行驶4h两车相遇; ③快车的速度为150km/h; ④行驶6h两车相距450km; ⑤相遇时慢车行驶了280km; ⑥行驶6h快车停止了行驶.其中符合图象描述的说法有( )个.