题目内容
3.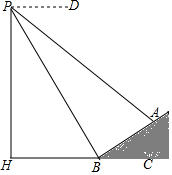 如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°,已知tan∠ABC=$\frac{\sqrt{3}}{3}$,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥BC,则A,B两点间的距离为( )米.
如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°,已知tan∠ABC=$\frac{\sqrt{3}}{3}$,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥BC,则A,B两点间的距离为( )米.| A. | 200$\sqrt{3}$ | B. | 200 | C. | 100$\sqrt{3}$ | D. | 100 |
分析 根据特殊角的正切值得到∠ABC=30°,得到∠PBA=90°,根据正弦的定义求出PB,根据正切的概念计算即可,
解答 解:∵tan∠ABC=$\frac{\sqrt{3}}{3}$,
∴∠ABC=30°,
由题意得,∠PBH=60°,
∴∠PBA=90°,
在Rt△PBH中,PB=$\frac{PH}{sin∠PBH}$=200$\sqrt{3}$,
在Rt△PBA中,AB=PB•tan∠APB=200,
故选:B.
点评 本题考查的是解直角三角形的应用,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
相关题目
16.已知代数式x+2y的值是-2,则代数式3x+6y+1的值是( )
| A. | -3 | B. | -5 | C. | 1 | D. | 3 |
14.若(m,a),(m+1,b)在直线y=-2x+3上,则a、b的大小关系为( )
| A. | a<b | B. | a=b | C. | a>b | D. | 无法确定 |
11.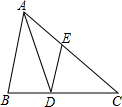 如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{CE}{AC}=\frac{3}{5}$,那么$\frac{AE}{AB}$的值为( )
如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{CE}{AC}=\frac{3}{5}$,那么$\frac{AE}{AB}$的值为( )
 如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{CE}{AC}=\frac{3}{5}$,那么$\frac{AE}{AB}$的值为( )
如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{CE}{AC}=\frac{3}{5}$,那么$\frac{AE}{AB}$的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
18.已知点M(1,m2+1)在双曲线y=$\frac{k}{x}$上,则双曲线y=$\frac{k}{x}$一定分布在( )象限.
| A. | 一、二 | B. | 一、三 | C. | 二、三 | D. | 二、四 |
8.下列运算中,正确的是( )
| A. | a2•a3=a6 | B. | a2+a3=a6 | C. | a6÷a2=a4 | D. | 2(a+b)=2a+b |
10.如果在△ABC中,∠A=70°-∠B,则∠C等于( )
| A. | 140° | B. | 110° | C. | 70° | D. | 35° |



