题目内容
13．
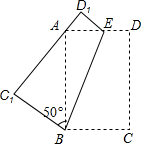如图，将一个矩形纸片ABCD，沿着BE折叠，使C、D两点分别落在点C1、D1处．若∠C1BA=50°，则∠ABE的度数为（ ）| A． | 10° | B． | 20° | C． | 30° | D． | 40° |
分析 根据折叠前后对应角相等即可得出∠CBE的度数，再根据∠ABC为直角即可得到答案．
解答 解：设∠ABE=x，
根据折叠前后角相等可知，∠C1BE=∠CBE=50°+x，
∵∠ABC=90°，
∴50°+x+x=90°，
解得x=20°．
故选B．
点评 本题考查图形的翻折变换，折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变．
练习册系列答案
名校课堂系列答案
相关题目
6．下列说法正确的是（ ）
| A． | -9在实数范围内没有平方根 | B． | $\sqrt{324}=±18$ | ||
| C． | ±6是216的立方根 | D． | 平方根等于其本身的数有0，1 |
4．
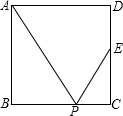如图，在正方形ABCD中，如果E为CD边的中点，P是BC边上的一动点，那么下列条件中，能推出△ABP与△ECP相似的是（ ）
如图，在正方形ABCD中，如果E为CD边的中点，P是BC边上的一动点，那么下列条件中，能推出△ABP与△ECP相似的是（ ）| A． | BP：BC=1：3 | B． | BP：BC=1：2 | C． | BP：BC=2：3 | D． | BP：BC=3：4 |
1．
如图，已知△ABC为直角三角形，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于（ ）
如图，已知△ABC为直角三角形，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于（ ）| A． | 90° | B． | 135° | C． | 270° | D． | 315° |
8．
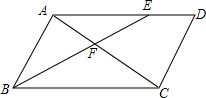如图，在?ABCD中，点E在AD边上，BE交对角线AC于点F，则下列各式错误的是（ ）
如图，在?ABCD中，点E在AD边上，BE交对角线AC于点F，则下列各式错误的是（ ）| A． | $\frac{AF}{CF}=\frac{EF}{BF}$ | B． | $\frac{AF}{BF}=\frac{EF}{CF}$ | C． | $\frac{BF}{BE}=\frac{CF}{AC}$ | D． | $\frac{AF}{EF}=\frac{CF}{BF}$ |
18．已知点M（1，m2+1）在双曲线y=$\frac{k}{x}$上，则双曲线y=$\frac{k}{x}$一定分布在（ ）象限．
| A． | 一、二 | B． | 一、三 | C． | 二、三 | D． | 二、四 |
5．下列运算正确的是（ ）
| A． | （ab）2=ab2 | B． | 3a+2a2=5a2 | C． | $\sqrt{（-4）^{2}}$=-4 | D． | a•a=a2 |
2．
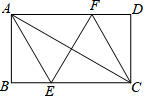如图，过矩形ABCD的对角线AC的中点O作EF⊥AC，交BC边于点E，交AD边于点F，分别连接AE、CF，若AB=2$\sqrt{3}$，∠DCF=30°，则EF的长为（ ）
如图，过矩形ABCD的对角线AC的中点O作EF⊥AC，交BC边于点E，交AD边于点F，分别连接AE、CF，若AB=2$\sqrt{3}$，∠DCF=30°，则EF的长为（ ）| A． | 4 | B． | 6 | C． | $\sqrt{3}$ | D． | 2$\sqrt{3}$ |
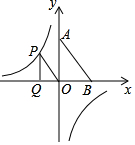在平面直角坐标系中，A（0，2），B（1，0），点P是反比例函数y=-$\frac{1}{x}$上的一个动点，过点P作PQ⊥x轴，垂足为Q，若以点O、P、Q为顶点的三角形与△OAB相似，则相应的点P有（ ）个．