题目内容
6.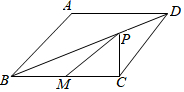 如图,菱形ABCD的边长为4cm,∠ABC=60°,且M为BC的中点,P是对角线BD上的一动点,则PM+PC的最小值为( )
如图,菱形ABCD的边长为4cm,∠ABC=60°,且M为BC的中点,P是对角线BD上的一动点,则PM+PC的最小值为( )| A. | 4 cm | B. | $\sqrt{3}$cm | C. | 2$\sqrt{5}$cm | D. | 2$\sqrt{3}$cm |
分析 根据菱形的性质,点A、C关于BD对称,连接AM即为PM+PC的最小值,再判断出△ABM是直角三角形,然后根据解直角三角形求出AM即可.
解答 解:如图,∵四边形ABCD是菱形,
∴点A、C关于BD对称,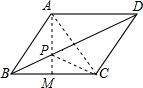
连接AM,AM即为PM+PC的最小值,
∵M是BC的中点,BC=2,
∴CM=BM=2,
∴AB=BC=2×2=4,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴△ABM是直角三角形,
∴AM=$\frac{\sqrt{3}}{2}$AB=2$\sqrt{3}$,
即PM+PC的最小值.
故选D.
点评 本题考查了菱形的性质,等边三角形的判定与性质,轴对称确定最短路线问题,熟记各性质并确定出PM+PC的最小值的点P的位置是解题的关键.

练习册系列答案
相关题目
19.两个袋子里分别装着写有1,2,3,4的四张完全相同的卡片,从每一袋子中各随机抽取一张,则两张卡片上数字之和等于6的概率是( )
| A. | $\frac{1}{16}$ | B. | $\frac{2}{16}$ | C. | $\frac{3}{16}$ | D. | $\frac{1}{2}$ |
17.若代数式2x2+3x-7的值是6,则代数式7-3x-2x2的值是( )
| A. | 6 | B. | -6 | C. | -7 | D. | 7 |
14.若(m,a),(m+1,b)在直线y=-2x+3上,则a、b的大小关系为( )
| A. | a<b | B. | a=b | C. | a>b | D. | 无法确定 |
1. 如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
 如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )| A. | 90° | B. | 135° | C. | 270° | D. | 315° |
11.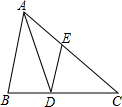 如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{CE}{AC}=\frac{3}{5}$,那么$\frac{AE}{AB}$的值为( )
如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{CE}{AC}=\frac{3}{5}$,那么$\frac{AE}{AB}$的值为( )
 如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{CE}{AC}=\frac{3}{5}$,那么$\frac{AE}{AB}$的值为( )
如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{CE}{AC}=\frac{3}{5}$,那么$\frac{AE}{AB}$的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
18.已知点M(1,m2+1)在双曲线y=$\frac{k}{x}$上,则双曲线y=$\frac{k}{x}$一定分布在( )象限.
| A. | 一、二 | B. | 一、三 | C. | 二、三 | D. | 二、四 |
15.下列说法正确的是( )
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 四边相等的四边形是菱形 | |
| C. | 矩形的对角线互相垂直 | |
| D. | 一组对边平行的四边形是平行四边形 |



