题目内容
10．
四个相同的小正方体搭建了一个积木，它的左视图和主视图均如图所示，则这堆积木不可能是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 由几何体的三视图即可得．
解答 解：D选项的左视图为
，不符合题目要求．
故选：D．
点评 本题主要考查由三视图判断几何体，由三视图想象几何体的形状，首先，应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，然后综合起来考虑整体形状．
练习册系列答案
相关题目
3．下列二次根式中，不是最简二次根式的是 （ ）
| A． | $\sqrt{5}$ | B． | $\sqrt{{a}^{2}+{b}^{2}}$ | C． | $\sqrt{\frac{1}{x}}$ | D． | $\sqrt{2a}$ |
1．
如图，已知△ABC为直角三角形，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于（ ）
如图，已知△ABC为直角三角形，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于（ ）| A． | 90° | B． | 135° | C． | 270° | D． | 315° |
18．已知点M（1，m2+1）在双曲线y=$\frac{k}{x}$上，则双曲线y=$\frac{k}{x}$一定分布在（ ）象限．
| A． | 一、二 | B． | 一、三 | C． | 二、三 | D． | 二、四 |
5．下列运算正确的是（ ）
| A． | （ab）2=ab2 | B． | 3a+2a2=5a2 | C． | $\sqrt{（-4）^{2}}$=-4 | D． | a•a=a2 |
2．
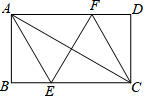如图，过矩形ABCD的对角线AC的中点O作EF⊥AC，交BC边于点E，交AD边于点F，分别连接AE、CF，若AB=2$\sqrt{3}$，∠DCF=30°，则EF的长为（ ）
如图，过矩形ABCD的对角线AC的中点O作EF⊥AC，交BC边于点E，交AD边于点F，分别连接AE、CF，若AB=2$\sqrt{3}$，∠DCF=30°，则EF的长为（ ）| A． | 4 | B． | 6 | C． | $\sqrt{3}$ | D． | 2$\sqrt{3}$ |
19．具备下列条件的△ABC中，不是直角三角形的是（ ）
| A． | ∠A+∠B=∠C | B． | ∠A：∠B：∠C=1：2：3 | C． | ∠A=∠B=2∠C | D． | ∠A=∠B=$\frac{1}{2}$∠C |
17．
某几何体的三视图如图所示，则这个几何体是（ ）
某几何体的三视图如图所示，则这个几何体是（ ）| A． | 圆柱 | B． | 长方体 | C． | 三棱锥 | D． | 三棱柱 |