题目内容
2．
如图，在平面直角坐标系中，AD=8，OD=OB，?ABCD的面积为24，求平行四边形的4个顶点的坐标．
分析 首先根据平行四边形的面积为24可求出BO的长，进而可得到OD，AO的长，则点A，D，B的坐标可求，再由平行四边形的性质即可求出点C的坐标．∵
解答 解：在平面直角坐标系中，?ABCD的面积为24，
∴AD•BO=24，
∵AD=8，
∴BO=3，
∵OD=OB，
∴OD=3，
∴AO=5，
∴A（-5，0），B（0，3），D（3，0）．
∵四边形ABCD是平行四边形，
∴BC∥AD，BC=AD=8，
∴C（8，3）．
点评 此题主要考查了平行四边形的性质以及勾股定理，正确得出AO的长是解题关键．
练习册系列答案
相关题目
12．-（-$\frac{1}{2}$）的倒数是（ ）
| A． | 2 | B． | $\frac{1}{2}$ | C． | -$\frac{1}{2}$ | D． | -2 |
作图题：如图，在△ABC所在的平面内找一点D，使D点到AB、AC两边的距离相等且到点A、点B的距离相等．（要求用尺规作图，保留作图痕迹）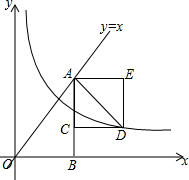
如图，点A在直线y=x上，AB⊥x轴于点B，点C在线段AB上，以AC为边作正方形ACDE，点D恰好在反比例函数y=$\frac{k}{x}$（k为常数，k≠0）第一象限的图象上，连接AD．若OA2-AD2=20，则k的值为10．