题目内容
14.化简二次根式:$\sqrt{\frac{{y}^{2}}{18x}}$(y>0)=$\frac{y\sqrt{2x}}{6x}$;$\sqrt{-24{a}^{3}}$=-2a$\sqrt{-6a}$.分析 直接利用二次根式的性质化简求出即可.
解答 解:$\sqrt{\frac{{y}^{2}}{18x}}$(y>0)=$\frac{\sqrt{{y}^{2}}}{\sqrt{18x}}$=$\frac{y}{3\sqrt{2x}}$=$\frac{y\sqrt{2x}}{6x}$;
$\sqrt{-24{a}^{3}}$=2$\sqrt{-6{a}^{3}}$=-2a$\sqrt{-6a}$.
故答案为:$\frac{y\sqrt{2x}}{6x}$;-2a$\sqrt{-6a}$.
点评 此题主要考查了二次根式的化简,正确掌握二次根式的性质是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在平面直角坐标系中,AD=8,OD=OB,?ABCD的面积为24,求平行四边形的4个顶点的坐标.
如图,在平面直角坐标系中,AD=8,OD=OB,?ABCD的面积为24,求平行四边形的4个顶点的坐标.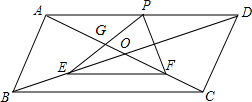 如图,?ABCD的对角线相交于点O,点E,F,P分别是OB,OC,AD的中点,分别连接EP,EF,PF,EP与AC相交于点G,且AC=2AB.
如图,?ABCD的对角线相交于点O,点E,F,P分别是OB,OC,AD的中点,分别连接EP,EF,PF,EP与AC相交于点G,且AC=2AB. 如图,抛物线经过A(-1,0),B(3,0),C(0,-3)三点,点P在第二象限的抛物线上,S△POB=S△PCO,求P点的坐标.
如图,抛物线经过A(-1,0),B(3,0),C(0,-3)三点,点P在第二象限的抛物线上,S△POB=S△PCO,求P点的坐标.