题目内容
17．已知：实数x满足（x2+x）2-（x2+x）-6=0，求：代数式x2+x+5的值．分析 设x2+x=t，则由原方程得到关于t的一元二次方程，通过解该方程得到x2+x的值；然后将其代入所求的代数式进行求值．
解答 解：设x2+x=t，则
t2-t-6=0，
整理，得
（t-3）（t+2）=0，
解得t=3或t=-2（舍去），
即x2+x=3，
所以x2+x+5=3+5=8，即x2+x+5的值为8．
点评 本题主要考查了换元法，即把某个式子看作一个整体，用一个字母去代替它，实行等量替换．
练习册系列答案
相关题目
根据如图所示的流程图计算，若输入x的值为-1，则输出y的值为8．
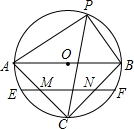如图，⊙O的直径AB=8，P是圆上任一点（A，B除外），∠APB的平分线交⊙O于C，弦EF过AC，BC的中点M，N，则EF的长是4$\sqrt{3}$．
如图，在平面直角坐标系中，AD=8，OD=OB，?ABCD的面积为24，求平行四边形的4个顶点的坐标．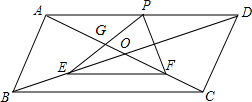
如图，?ABCD的对角线相交于点O，点E，F，P分别是OB，OC，AD的中点，分别连接EP，EF，PF，EP与AC相交于点G，且AC=2AB．