题目内容
5. 如图,在矩形ABCD中,对角线AC、BD交于点O,过顶点C作BD的平行线交AD的延长线于点E,△ACE是什么三角形?说明你的理由.
如图,在矩形ABCD中,对角线AC、BD交于点O,过顶点C作BD的平行线交AD的延长线于点E,△ACE是什么三角形?说明你的理由.
分析 根据矩形的性质求出AC=BD,AD∥BC,根据平行四边形的判定推出四边形DECB是平行四边形,根据平行四边形的性质得出BD=CE即可.
解答 解:△ACE是等腰三角形;理由:
∵四边形ABCD是矩形,
∴AC=BD,AD∥BC,
即DE∥BC,
∵BD∥CE,
∴四边形DECB是平行四边形,
∴BD=CE,
∴AC=CE,
∴△ACE是等腰三角形.
点评 本题考查了矩形的性质,平行四边形的判定和性质,等腰三角形的判定的应用,解此题的关键是求出AC=BD和得出四边形DECB是平行四边形.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
15.如果三角形的两边分别为3和5,那么第三边可能是( )
| A. | 3 | B. | 1 | C. | 2 | D. | 8 |
20. 如图,点A,B,C在⊙O上,∠A=36°,∠B=64°,则∠C的度数为( )
如图,点A,B,C在⊙O上,∠A=36°,∠B=64°,则∠C的度数为( )
 如图,点A,B,C在⊙O上,∠A=36°,∠B=64°,则∠C的度数为( )
如图,点A,B,C在⊙O上,∠A=36°,∠B=64°,则∠C的度数为( )| A. | 28° | B. | 32° | C. | 44° | D. | 52° |
14. 如图,矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为( )
如图,矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为( )
 如图,矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为( )
如图,矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为( )| A. | 28 | B. | 20 | C. | 16 | D. | 14 |
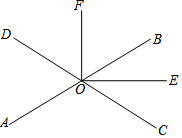 如图所示,直线AB,CD相交于点O,OE平分∠BOC,OF⊥OE,且∠AOC=114°,求∠BOF的度数.
如图所示,直线AB,CD相交于点O,OE平分∠BOC,OF⊥OE,且∠AOC=114°,求∠BOF的度数.