题目内容
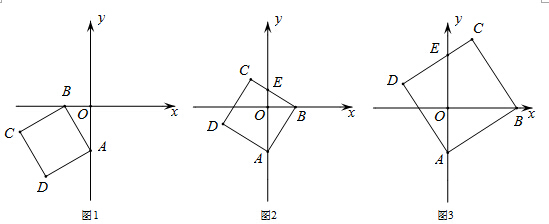
11.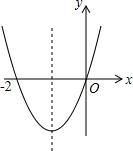 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法:①c=0;②该抛物线的对称轴是直线x=-1;③当x=1时,y=2n;④am2+bn+a>0(a≠-1).其中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法:①c=0;②该抛物线的对称轴是直线x=-1;③当x=1时,y=2n;④am2+bn+a>0(a≠-1).其中正确的是( )| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
分析 由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:∵抛物线与y轴交于原点,
∴c=0,故①正确;
∵抛物线与x轴的交点为(-2,0),(0,0),
∴该抛物线的对称轴是:直线x=$\frac{-2+0}{2}$=-1,故②正确;
当x=1时,y=a+b+c
∵对称轴是直线x=-1,
∴-$\frac{b}{2a}$=-1,b=2a,
又∵c=0,
∴y=3a,故③错误;
∵x=m对应的函数值为y=am2+bm+c,x=-1对应的函数值为y=a-b+c,
又∵x=-1时函数取得最小值,
∴a-b+c<am2+bm+c,即a-b<am2+bm,
∵b=2a,
∴am2+bm+a>0(m≠-1).故④正确.
故选:C.
点评 本题考查了二次函数图象与系数的关系.二次函数y=ax2+bx+c(a≠0)系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定.

练习册系列答案
相关题目

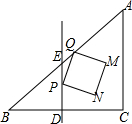 如图,在△ABC中,∠C=90°,AC=BC=12cm,D为BC边中点.DE⊥BC交边AB于点E.点P从点E出发.以1cm/s的速度沿ED向终点D运动.同时点Q从点E出发,以$\sqrt{2}$cm/s的速度沿EA向终点A运动.以PQ为边在∠AED的内部作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(cm2).点P的运动时间为t(s).
如图,在△ABC中,∠C=90°,AC=BC=12cm,D为BC边中点.DE⊥BC交边AB于点E.点P从点E出发.以1cm/s的速度沿ED向终点D运动.同时点Q从点E出发,以$\sqrt{2}$cm/s的速度沿EA向终点A运动.以PQ为边在∠AED的内部作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(cm2).点P的运动时间为t(s).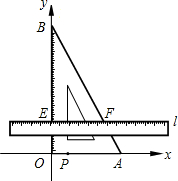 如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3$\sqrt{3}$).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动,速度分别为1,$\sqrt{3}$,2(长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以$\frac{\sqrt{3}}{3}$(长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3$\sqrt{3}$).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动,速度分别为1,$\sqrt{3}$,2(长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以$\frac{\sqrt{3}}{3}$(长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.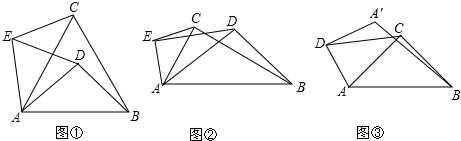
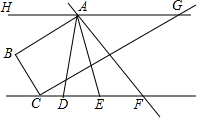 如图,已知AB⊥CB,垂足为B,CG⊥BC,垂足为C,∠BAH=∠GCF=30°,AD平分∠BAF,AE平分∠BAG.
如图,已知AB⊥CB,垂足为B,CG⊥BC,垂足为C,∠BAH=∠GCF=30°,AD平分∠BAF,AE平分∠BAG.