题目内容
6.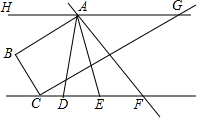 如图,已知AB⊥CB,垂足为B,CG⊥BC,垂足为C,∠BAH=∠GCF=30°,AD平分∠BAF,AE平分∠BAG.
如图,已知AB⊥CB,垂足为B,CG⊥BC,垂足为C,∠BAH=∠GCF=30°,AD平分∠BAF,AE平分∠BAG.(1)求∠EAG的度数;
(2)求证:HG∥CF;
(3)试判断∠DAE与∠AFC之间的数量关系,并说明理由.
分析 (1)根据平角的定义和角平分线的定义即可得到结论;
(2)根据已知条件得到AB∥CG,由平行线的性质得到∠AGC=∠HAB=30°,等量代换得到∠AGC=∠GCF,根据平行线的判定定理即可得到结论;
(3)根据AD平分∠BAF,AE平分∠BAG,得到∠BAE=∠GAE,∠BAD=∠FAD=x+y,于是得到∠GAF=2x=2∠DAE,根据平行线的性质得到∠AFC=∠GAF,等量代换即可得到结论.
解答 解:(1)∵∠BAH=30°,
∴∠BAG=180°-30°=150°,
∵AE平分∠BAG,
∴∠EAG=$\frac{1}{2}∠$BAG=75°;
(2)∵AB⊥CB,垂足为B,CG⊥BC,垂足为C,
∴AB∥CG,
∴∠AGC=∠HAB=30°,
∵∠BAH=∠GCF=30°,
∴∠AGC=∠GCF,
∴HG∥CF;
(3)∠AFC=2∠DAE,
理由:设∠DAE=x,∠EAF=y,
∵AD平分∠BAF,AE平分∠BAG,
∴∠BAE=∠GAE,∠BAD=∠FAD=x+y,
∴x+y+x=y+∠GAF,
∴∠GAF=2x=2∠DAE,
∵HG∥CF,
∴∠AFC=∠GAF,
∴∠AFC=2∠DAE.
点评 本题考查了平行线的判定和性质,角平分线的定义,熟练掌握平行线的判定定理是解题的关键.

练习册系列答案
相关题目
11.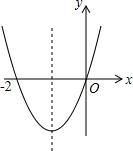 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法:①c=0;②该抛物线的对称轴是直线x=-1;③当x=1时,y=2n;④am2+bn+a>0(a≠-1).其中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法:①c=0;②该抛物线的对称轴是直线x=-1;③当x=1时,y=2n;④am2+bn+a>0(a≠-1).其中正确的是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法:①c=0;②该抛物线的对称轴是直线x=-1;③当x=1时,y=2n;④am2+bn+a>0(a≠-1).其中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法:①c=0;②该抛物线的对称轴是直线x=-1;③当x=1时,y=2n;④am2+bn+a>0(a≠-1).其中正确的是( )| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
17.在Rt△ABC中,∠ACB=90°,AC=$\sqrt{2}$,BC=2,则AB的长为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\sqrt{2}$ | D. | 6 |
16.在Rt△ABC中,∠C=90°,若tanA=$\frac{3}{4}$,则sinB的值是( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{3}$ |