题目内容
19.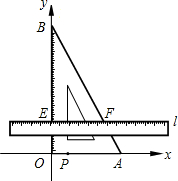 如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3$\sqrt{3}$).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动,速度分别为1,$\sqrt{3}$,2(长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以$\frac{\sqrt{3}}{3}$(长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3$\sqrt{3}$).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动,速度分别为1,$\sqrt{3}$,2(长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以$\frac{\sqrt{3}}{3}$(长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.请解答下列问题:
(1)过A,B两点的直线解析式是y=-$\sqrt{3}$x+3$\sqrt{3}$,∠BAO=60°;
(2)当t﹦4时,点P的坐标为(0,$\sqrt{3}$);当t﹦$\frac{9}{2}$,点P与点E重合;
(3)作点P关于直线EF的对称点P′.在运动过程中,若形成的四边形PEP′F为菱形,则t的值是多少?
分析 (1)设过A,B两点的直线解析式是y=kx+b,利用待定系数法求出直线解析式,根据直角三角形的性质求出∠BAO;
(2)根据题意列出算式求出OP的长度即可;
(3)分点P在在AO,OB,BA上三种情况,根据菱形的判定和性质,结合锐角三角函数的定义计算即可.
解答 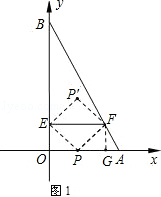 解:(1)设过A,B两点的直线解析式是y=kx+b,
解:(1)设过A,B两点的直线解析式是y=kx+b,
$\left\{\begin{array}{l}{b=3\sqrt{3}}\\{3k+b=0}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-\sqrt{3}}\\{b=3\sqrt{3}}\end{array}\right.$,
∴直线AB解析式是y=-$\sqrt{3}$x+3$\sqrt{3}$,
∵∠B=30°,
∴∠BAO=60°,
故答案为:y=-$\sqrt{3}$x+3$\sqrt{3}$;60°;
(2)当t﹦4时,OP=(4-3)×$\sqrt{3}$=$\sqrt{3}$,
∴点P的坐标为(0,$\sqrt{3}$);
当点P与点E重合时,(t-3)×$\sqrt{3}$=$\frac{\sqrt{3}}{3}$t,
解得,t=$\frac{9}{2}$
∴t=$\frac{9}{2}$,点P与点E重合;
故答案为:(0,$\sqrt{3}$);$\frac{9}{2}$;
(3)①当点P在线段AO上时,过F作FG⊥x轴,G为垂足(如图1)
∵OE=FG,EP=FP,∠EOP=∠FGP=90°,
∴△EOP≌△FGP(SAS),
∴OP=PG,
又∵OE=FG=$\frac{\sqrt{3}}{3}$t,∠A=60°,
∴AG=FGtan60°=$\frac{1}{3}$t;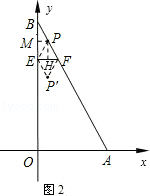
而AP=t,
∴OP=3-t,PG=AP-AG=$\frac{2}{3}$t,
由3-t=$\frac{2}{3}$t,得t=$\frac{9}{5}$;
当点P在线段OB上时,形成的是三角形,不存在菱形;
当点P在线段BA上时,
过P作PH⊥EF,PM⊥OB,H、M分别为垂足(如图2),则四边形PMEH是矩形,
∴PM=EH.
∵四边形PEP'F是菱形,
∴EH=FH.
∵OE=$\frac{\sqrt{3}}{3}$t,
∴BE=3$\sqrt{3}$-$\frac{\sqrt{3}}{3}$t,
∴EF=BEtan60°=3-$\frac{t}{3}$,
∴MP=EH=$\frac{1}{2}$EF=$\frac{9-t}{6}$,又BP=2(t-6),
在Rt△BMP中,BP•cos60°=MP
即2(t-6)•$\frac{1}{2}$=$\frac{9-t}{6}$,
解得t=$\frac{45}{7}$.
点评 本题考查的是菱形的判定和性质、待定系数法求函数解析式、全等三角形的判定和性质、锐角三角函数的概念,正确作出辅助性、灵活运用相关的性质定理和判定定理是解题的关键,注意分情况讨论思想的运用.

| A. | 1×106米 | B. | 1×10-5米 | C. | 1×10-6米 | D. | 1×105米 |
| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | 15,8,17 | C. | 13,14,15 | D. | $\frac{3}{5}$,$\frac{4}{5}$,1 |
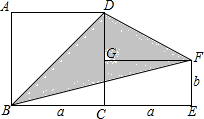 如图,正方形ABCD的边长为a,面积为6;长方形CEFG的长、宽分别为a,b,长方形的面积为2,其中点B、C、E在同一直线上,连接DF.求△BDF的面积.
如图,正方形ABCD的边长为a,面积为6;长方形CEFG的长、宽分别为a,b,长方形的面积为2,其中点B、C、E在同一直线上,连接DF.求△BDF的面积.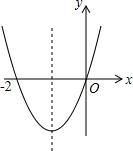 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法:①c=0;②该抛物线的对称轴是直线x=-1;③当x=1时,y=2n;④am2+bn+a>0(a≠-1).其中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法:①c=0;②该抛物线的对称轴是直线x=-1;③当x=1时,y=2n;④am2+bn+a>0(a≠-1).其中正确的是( )