题目内容
1.(1)问题探究:如图1,△ABC、△ADE均为等边三角形,连接BD、CE,则线段BD与CE的数量关系是相等.
(2)类比延伸
如图2,在Rt△ABC和Rt△ADE中,∠ACB=∠AED=90°,∠ABC=∠ADE=30°,连接BD、CE,试确定BD与CE的数量关系,并说明理由.
(3)拓展迁移
如图3,在四边形ABCD中,AC⊥BC,且AC=BC,CD=4,若将线段DA绕点D按逆时针方向旋转90°得到DA′,连接BA′,则线段BA′的长度是4$\sqrt{2}$.
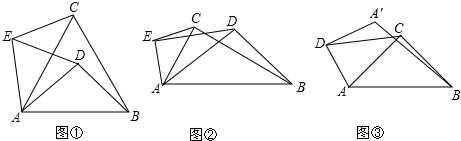
分析 (1)由等边三角形的性质可得AC=AB,AE=AD,∠EAD=∠CAB=60°,可得∠EAC=∠DAB,易得△EAC≌△DAB,由全等三角形的性质可得BD=CE;
(2)根据三角形的内角和和直角三角形的性质得到∠EAD=∠CAB=60°,AD=2AE,AB=2AC,推出△EAD∽△CAB,得到$\frac{AE}{AD}=\frac{AC}{AB}$,于是得到△EAC∽△DAB,求得$\frac{BD}{CE}=\frac{AD}{AE}$=2,即可得到结论;
(3)首先证明△ABC和△AA′D为等腰直角三角形,从而求得AB:AC=$\sqrt{2}$,$\frac{AA′}{AD}=\frac{AB}{AC}$,然后再证明∠A′AB=∠DAC,从而可证明△CAD∽△BA′A,最后利用相似三角形的性质可求得A′B的长度.
解答 解:(1)∵△ABC、△ADE均为等边三角形,
∴AC=AB,AE=AD,∠EAD=∠CAB=60°,
∴∠EAC=60°-∠CAD,∠DAB=60°-∠CAD,
∴∠EAC=∠DAB,
在△EAC与△DAB中,
$\left\{\begin{array}{l}{AE=AD}\\{∠EAC=∠DAB}\\{AC=AB}\end{array}\right.$,
∴△EAC≌△DAB,
∴BD=CE;
(2)BD=2CE,
理由:∵∠ACB=∠AED=90°,∠ABC=∠ADE=30°,
∴∠EAD=∠CAB=60°,AD=2AE,AB=2AC,
∴∠EAC=∠DAB,△EAD∽△CAB,
∴$\frac{AE}{AD}=\frac{AC}{AB}$,
∴△EAC∽△DAB,
∴$\frac{BD}{CE}=\frac{AD}{AE}$=2,
∴BD=2CE;
(3)连接A′A,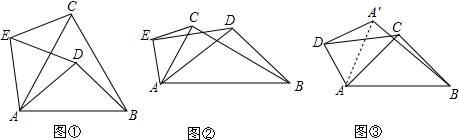 如图③,
如图③,
∵AC⊥BC,且AC=BC,
∴△ABC为等腰直角三角形.
∴$\frac{AB}{AC}=\sqrt{2}$,
∵将线段DA绕点D按逆时针方形旋转90°得到DA′
∴△AA′D为等腰直角三角形.
∴△ABC∽△AA′D.
∴$\frac{AA′}{AD}=\frac{AB}{AC}$,
又∵∠CAB=∠A′AD,
∴∠A′AB=∠DAC,
∵$\frac{AA′}{AD}=\frac{AB}{AC}$,
∴$\frac{AA′}{AB}=\frac{AD}{AC}$,
∴△CAD∽△BA′A.
∴$\frac{A′B}{CD}=\frac{AB}{AC}$,即$\frac{A′B}{4}=\sqrt{2}$,
∴A′B=4$\sqrt{2}$.
故答案为:4$\sqrt{2}$.
点评 本题主要考查的是旋转的性质、等腰三角形的性质、全等三角形的性质及判定定理、相似三角形的性质和判定,证得相似三角形是解题的关键.

| A. | 1×106米 | B. | 1×10-5米 | C. | 1×10-6米 | D. | 1×105米 |
| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | 15,8,17 | C. | 13,14,15 | D. | $\frac{3}{5}$,$\frac{4}{5}$,1 |
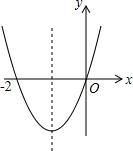 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法:①c=0;②该抛物线的对称轴是直线x=-1;③当x=1时,y=2n;④am2+bn+a>0(a≠-1).其中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法:①c=0;②该抛物线的对称轴是直线x=-1;③当x=1时,y=2n;④am2+bn+a>0(a≠-1).其中正确的是( )| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
| A. | $\sqrt{2}$ | B. | ±$\sqrt{2}$ | C. | ±2 | D. | 2 |