题目内容
1.如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
(1)观察图形,你能写出(m+n)2,(m-n)2,mn这三个代数式之间的等量关系吗?
(2)根据(1)中的等量关系,解决如下问题:若a+b=5,ab=4,求a-b的值.
分析 (1)直接利用图形中阴影部分面积得出等式;
(2)利用(1)中所求,结合完全平方公式求出答案.
解答 解:(1)如图所示:(m+n)2-4mn=(m-n)2;
(2)(a-b)2=(a+b)2-4ab,
∵a+b=5,ab=4,
∴(a-b)2=25-16=9,
∴a-b=±3.
点评 此题主要考查了完全平方公式的几何背景,正确利用图形面积得出等量关系是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
16.下列语句正确的是( )
| A. | 如果一个数的立方根是这个数本身,那么这个数一定是0 | |
| B. | 一个数的立方根不是正数就是负数 | |
| C. | 负数没有立方根 | |
| D. | 一个不为零的数的立方根和这个数同号,0的立方根是0 |
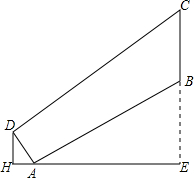 如图,在一坡长AB为$70\sqrt{5}$,坡度i1=1:2的山顶B处修建一座铁塔BC,小李在其对面山坡沿坡面AD向上走了25米到D处测得塔顶C的仰角为37°,已知山坡AD的坡度i2=1:0.75
如图,在一坡长AB为$70\sqrt{5}$,坡度i1=1:2的山顶B处修建一座铁塔BC,小李在其对面山坡沿坡面AD向上走了25米到D处测得塔顶C的仰角为37°,已知山坡AD的坡度i2=1:0.75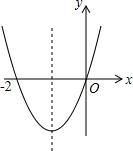 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法:①c=0;②该抛物线的对称轴是直线x=-1;③当x=1时,y=2n;④am2+bn+a>0(a≠-1).其中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法:①c=0;②该抛物线的对称轴是直线x=-1;③当x=1时,y=2n;④am2+bn+a>0(a≠-1).其中正确的是( )