题目内容
20.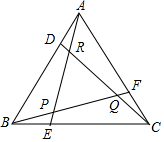 如图,△ABC是边长为m的正三角形,D,E,F分别在边AB,BC,CA上,AE,BF交于点P,BF,CD交于点Q,CD,AE交于点R,若$\frac{AD}{AB}$=$\frac{BE}{BC}$=$\frac{CF}{CA}$=k(0<k<$\frac{1}{2}$).
如图,△ABC是边长为m的正三角形,D,E,F分别在边AB,BC,CA上,AE,BF交于点P,BF,CD交于点Q,CD,AE交于点R,若$\frac{AD}{AB}$=$\frac{BE}{BC}$=$\frac{CF}{CA}$=k(0<k<$\frac{1}{2}$).(1)求∠PQR的度数;
(2)求证:△ARD∽△ABE;
(3)求△PQR与△ABC的面积之比(用含k的代数式表示)
分析 (1)只要证明△ABP≌△BCQ≌△CAR,推出∠APB=∠BQC=∠ARC,推出180°-∠APB=180°-BQC=180°-ARC,即∠RPQ=∠PQR=∠PRQ,由此即可解决问题.
(2)只要证明∠ARD=∠ABE=60°即可解决问题.
(3)想办法求出等边三角形△PQR与△ABC的边长即可解决问题.
解答 解:(1)∵$\frac{AD}{AB}$=$\frac{BE}{BC}$=$\frac{CF}{CA}$=k,△ABC是等边三角形,
∴AB=CB=AC,∠ABC=∠BAC=∠ACB=60°,AD=BE=CF,
∴△ABE≌△BCF≌△CAD,
∴∠BAE=∠CBQ=∠ACD,∴∠ABP=∠BCQ=∠CAR,
∴△ABP≌△BCQ≌△CAR,
∴∠APB=∠BQC=∠ARC,
∴180°-∠APB=180°-BQC=180°-ARC,
即∠RPQ=∠PQR=∠PRQ,
∵∠RPQ+∠PQR+∠PRQ=180°,
∴∠RPQ=∠PQR=∠PRQ=60°.
∴∠PQR=60°.
(2)∵△PQR是等边三角形,
∴∠PRQ=60°,
∴∠ARD=∠PRQ=60°,
∴∠ARD=∠ABC=∠ABE,
∵∠DAR=∠EAB,
∴△ARD∽△ABE.
(3)作AH⊥BC于H.易知BH=CH=$\frac{m}{2}$,AH=$\frac{\sqrt{3}}{2}$m,BE=km,EH=$\frac{1}{2}$m-km,
在Rt△AEH中,AE=$\sqrt{A{H}^{2}+E{H}^{2}}$=$\sqrt{{k}^{2}-k+1}$•m,
∵△ARD∽△ABE,
∴$\frac{AR}{m}$=$\frac{RD}{km}$=$\frac{km}{AE}$,
∴AR=$\frac{k}{\sqrt{{k}^{2}-k+1}}$•m,RD=$\frac{{k}^{2}}{\sqrt{{k}^{2}-k+1}}$•m,PE=RD=$\frac{{k}^{2}}{\sqrt{{k}^{2}-k+1}}$•m,
∴AP=AE-PE=$\frac{1-k}{\sqrt{{k}^{2}-k+1}}$•m,
当0<k<$\frac{1}{2}$时,RP=AP-AR=$\frac{1-2k}{\sqrt{{k}^{2}-k+1}}$•m,
∵△PQR,△ABC都是等边三角形,
∴$\frac{{S}_{△PQR}}{{S}_{△ABC}}$=$\frac{\frac{\sqrt{3}}{4}(\frac{1-2k}{\sqrt{{k}^{2}-k+1}}m)^{2}}{\frac{\sqrt{3}}{4}{m}^{2}}$=$\frac{(1-2k)^{2}}{{k}^{2}-k+1}$.
点评 本题考查相似三角形综合题、等边三角形的判定和性质、全等三角形的判定和性质、勾股定理.等边三角形的面积等知识,解题的关键是熟练掌握全等三角形的判定和性质,学会添加常用辅助线,构造直角三角形解决问题,属于中考压轴题.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案| A. | -6是36的一个平方根 | B. | 任何正数都有两个平方根 | ||
| C. | (-8)2的平方根是8 | D. | 正数的两个平方根是一对相反数 |
| A. | a>b>c | B. | c>a>b | C. | a>c>b | D. | c>b>a |
| A. | $\frac{6}{5}$ | B. | $\frac{5}{6}$ | C. | $\frac{9}{5}$ | D. | $\frac{5}{9}$ |
 在?ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
在?ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.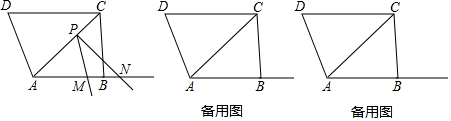
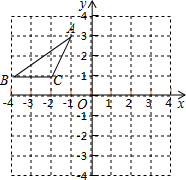 如图,在平面直角坐标系中,点A、B、C的坐标分别为(-1,3)、(-4,1)(-2,1),先将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2,点A1的对应点为点A2.
如图,在平面直角坐标系中,点A、B、C的坐标分别为(-1,3)、(-4,1)(-2,1),先将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2,点A1的对应点为点A2.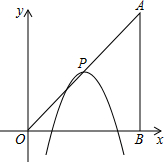 如图,在平面直角坐标系中,点A,B的坐标分别为(6,6),(6,0),抛物线y=-(x-m)2+n的顶点P在折线OA-AB上运动.
如图,在平面直角坐标系中,点A,B的坐标分别为(6,6),(6,0),抛物线y=-(x-m)2+n的顶点P在折线OA-AB上运动.