题目内容
15.如图,在梯形ABCD中,AB∥DC且∠ABC=90°,AB=24,BC=18,P为锑形ABCD的对角线AC上的一点,AP=20,以P为顶点的∠MPN的两边分别交射线AB于M、N两点,且∠MPN=∠CAB.设AM=x,AN=y(y>x>0).(1)求y与x之间的关系式,并写出x的取值范围;
(2)当x取何值时,直径为AM的⊙O1与直径为PC的⊙O2相切?
(3)若直线PM、PN与边DC分别相交于点E,F,当△PEF为等腰三角形时,直接写出x的值.
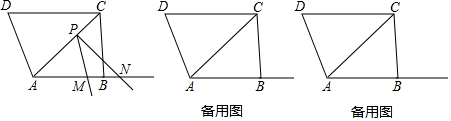
分析 (1)如图1中,作PH⊥AB于H.在Rt△ABC中,可得AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{2{4}^{2}+1{8}^{2}}$=30,由PH∥BC,PH=20,推出$\frac{PH}{BC}$=$\frac{AP}{AC}$=$\frac{AH}{AB}$,可得PH=12,AH=16,由△NPM∽△NAP,推出PN2=NM•NA,推出PH2+HN2=NM•NA,可得122+(y-16)2=(y-x)•y,由此即可解决问题.
(2)如图2中,作O2K⊥AB于K,根据两圆相切时,圆心距等于半径之和,列出方程即可解决问题.
(3)分三种情形讨论①如图3中,当EF=EP时,构建方程组解决问题,构建方程组解决问题.②如图4中,当PE=PF时.③如图5中,当FP=FE时,易知点M与点A重合,此时x=0.
解答 解:(1)如图1中,作PH⊥AB于H.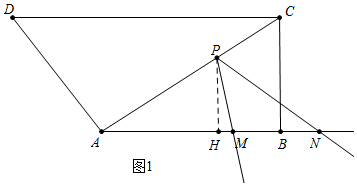
在Rt△ABC中,∵∠ABC=90°,AB=24,BC=18,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{2{4}^{2}+1{8}^{2}}$=30,
∵PH∥BC,PH=20,
∴$\frac{PH}{BC}$=$\frac{AP}{AC}$=$\frac{AH}{AB}$,
∴PH=12,AH=16,
∵∠NPM=∠PAN,∠PNM=∠PNA,
∴△NPM∽△NAP,
∴PN2=NM•NA,
∴PH2+HN2=NM•NA,
∴122+(y-16)2=(y-x)•y,
∴y=$\frac{400}{32-x}$(0≤x<32).
(2)如图2中,作O2K⊥AB于K,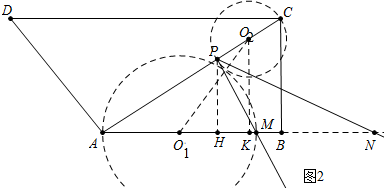
∵O2K∥BC,
∴$\frac{{O}_{2}K}{BC}$=$\frac{A{O}_{2}}{AC}$=$\frac{AK}{AB}$,
∴AK=20,O2K=15,
在Rt△O1O2K中,O1O2=$\sqrt{{O}_{2}{K}^{2}+{O}_{1}{K}^{2}}$=$\sqrt{1{5}^{2}+(20-\frac{1}{2}x)^{2}}$,
当两圆相切时,O1O2=5+$\frac{1}{2}$x,
∴152+(20-x)2=(5+$\frac{1}{2}$x)2,
解得x=24.
∴当x为24时,⊙O1与⊙O2相切.
(3)①如图3中,当EF=EP时,
∵CD∥AN,
∴∠EFP=∠PNM,
∵∠EFP=∠EPF=∠NPM=∠PAN,
∴PA=PN,∵PH⊥AN,
∴AH=HN=20,
∴y=AN=40,
∴40=$\frac{400}{32-x}$,
∴x=22.
②如图4中,当PE=PF时.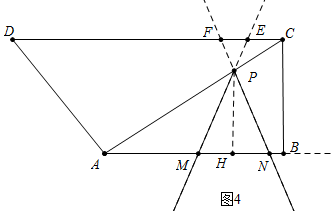
易证PM=PN,∵PH⊥NM,
∴HM=HN,
∴20-x=y-20,
∴y=40-x,
∴40-x=$\frac{400}{32-x}$,
解得X=36-4$\sqrt{26}$或36+4$\sqrt{26}$(舍弃),
∴x=36-4$\sqrt{26}$.
③如图5中,当FP=FE时,易知点M与点A重合,此时x=0.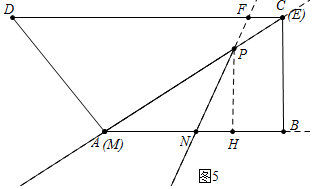
综上所述,当△PEF为等腰三角形时,x的值为0或22或36-4$\sqrt{26}$.
点评 本题考查圆综合题、相似三角形的判定和性质、平行线分线段成比例定理、等腰三角形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,学会构建方程组解决问题,属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案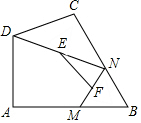 如图,在四边形ABCD中,∠A=90°,AB=3,AD=$\sqrt{7}$,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( )
如图,在四边形ABCD中,∠A=90°,AB=3,AD=$\sqrt{7}$,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( )| A. | $\sqrt{7}$ | B. | 4 | C. | 3 | D. | 2 |
| A. | 条形统计图 | B. | 折线统计图 | C. | 扇形统计图 | D. | 频数分布直方图 |
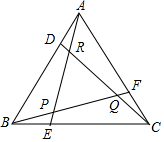 如图,△ABC是边长为m的正三角形,D,E,F分别在边AB,BC,CA上,AE,BF交于点P,BF,CD交于点Q,CD,AE交于点R,若$\frac{AD}{AB}$=$\frac{BE}{BC}$=$\frac{CF}{CA}$=k(0<k<$\frac{1}{2}$).
如图,△ABC是边长为m的正三角形,D,E,F分别在边AB,BC,CA上,AE,BF交于点P,BF,CD交于点Q,CD,AE交于点R,若$\frac{AD}{AB}$=$\frac{BE}{BC}$=$\frac{CF}{CA}$=k(0<k<$\frac{1}{2}$).