题目内容
8．若一个圆锥底面圆的半径为3cm，高为4cm，则这个圆锥的侧面积为15πcm2．（结果保留π）分析 先利用勾股定理计算出圆锥的母线长，然后根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形的面积公式计算这个圆锥的侧面积．
解答 解：这个圆锥的母线长=$\sqrt{{3}^{2}+{4}^{2}}$=5，
所以这个圆锥的侧面积=$\frac{1}{2}$•2π•3•5=15π（cm2）．
故答案为15π．
点评 本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．
练习册系列答案
相关题目
由于发生山体滑坡灾害，武警救援队火速赶往灾区救援，探测出某建筑物废墟下方点C处有生命迹象．在废墟一侧地面上探测点A、B相距2米，探测线与该面的夹角分别是30°和45°（如图），试确定生命所在点C的深度（参考数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732，结果精确到0.1）
16．计算-3-（-2）的结果等于（ ）
| A． | 1 | B． | 5 | C． | -5 | D． | -1 |
3．
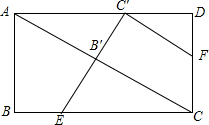如图，在矩形ABCD中，点E在BC上，将△ABE沿AE翻折，点B恰好落在对角线AC上的B′处，点F在CD上，将△ECF沿EF翻折，点C恰好落在AD上的C′处，若E、B′C′三点共线，则$\frac{CF}{AB}$=（ ）
如图，在矩形ABCD中，点E在BC上，将△ABE沿AE翻折，点B恰好落在对角线AC上的B′处，点F在CD上，将△ECF沿EF翻折，点C恰好落在AD上的C′处，若E、B′C′三点共线，则$\frac{CF}{AB}$=（ ）| A． | $\frac{\sqrt{2}}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{3}{4}$ |
13．
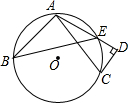如图，点A，B，C是⊙O上三点，AD和过C点的切线互相垂直，垂足为D，AD交⊙O于点E，若CD=3，AC=5，则cos∠ABE的值为（ ）
如图，点A，B，C是⊙O上三点，AD和过C点的切线互相垂直，垂足为D，AD交⊙O于点E，若CD=3，AC=5，则cos∠ABE的值为（ ）| A． | $\frac{7}{12}$ | B． | $\frac{7}{24}$ | C． | $\frac{24}{25}$ | D． | $\frac{16}{25}$ |
如图所示的两段弧中，位于上方的弧半径为r上，下方的弧半径为r下，则r上＜r下．（填“＜”“=”“＞”）
17．
如图，一艘轮船在诲面上由南向北航行，当它行驶到A处时，发现它的东北方向有一座灯塔B，轮船继续向北航行24海里后到达C处，发现灯塔B在它的北偏东75°方向，则此时轮船与灯塔B的距离是（ ）
如图，一艘轮船在诲面上由南向北航行，当它行驶到A处时，发现它的东北方向有一座灯塔B，轮船继续向北航行24海里后到达C处，发现灯塔B在它的北偏东75°方向，则此时轮船与灯塔B的距离是（ ）| A． | 24$\sqrt{2}$海里 | B． | 12$\sqrt{2}$海里 | C． | 24$\sqrt{3}$海里 | D． | 12$\sqrt{3}$海里 |
18．
如图，一扇形纸扇完全打开后，外侧两竹条AB和AC的夹角为120°，AB长为25cm，贴纸部分的宽BD为15cm，若纸扇两面贴纸，则贴纸的面积为（ ）
如图，一扇形纸扇完全打开后，外侧两竹条AB和AC的夹角为120°，AB长为25cm，贴纸部分的宽BD为15cm，若纸扇两面贴纸，则贴纸的面积为（ ）| A． | 175πcm2 | B． | 350πcm2 | C． | $\frac{800}{3}$πcm2 | D． | 150πcm2 |