题目内容
8.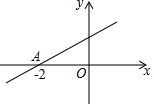 如图,直线y=kx+b与x轴的交点为A(-2,0),则不等式kx+b>0的解集为( )
如图,直线y=kx+b与x轴的交点为A(-2,0),则不等式kx+b>0的解集为( )| A. | x>2 | B. | x≤2 | C. | x>-2 | D. | x≤-2 |
分析 观察函数图象得到当x>-2时,函数图象在x轴上方,所以y>0,即kx+b>0.
解答 解:当x>-2时,y>0,即kx+b>0,
所以关于x的不等式kx+b>0的解集为x>-2.
故选C.
点评 本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
相关题目
3. 某区八年级有3000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:
某区八年级有3000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:
请你根据以上的信息,回答下列问题:
(1)a=0.05,b=40.
(2)在扇形统计图中,“成绩x满足50≤x<60“对应扇形的圆心角度数是18°;
(3)若将得分转化为等级,规定:50≤x<60评为D,60≤x<70评为C,70≤x<90评为B,90≤x<100评为A.这次全区八年级参加竞赛的学生约有1530人参赛成绩被评为“B”.
 某区八年级有3000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:
某区八年级有3000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:| 成绩x(分) | 频数 | 频率 |
| 50≤x<60 | 10 | a |
| 60≤x<70 | 16 | 0.08 |
| 70≤x<80 | b | 0.20 |
(1)a=0.05,b=40.
(2)在扇形统计图中,“成绩x满足50≤x<60“对应扇形的圆心角度数是18°;
(3)若将得分转化为等级,规定:50≤x<60评为D,60≤x<70评为C,70≤x<90评为B,90≤x<100评为A.这次全区八年级参加竞赛的学生约有1530人参赛成绩被评为“B”.
20. 在平面直角坐标系中,O为原点,点A(-3,0),点B(0,3),点E、点F分别为OA,OB的中点,若正方形OEDF绕点O顺时针旋转,得到正方形OE′D′F′,若直线AE′与直线BF′相交于点P,则点P的纵坐标的最大值是( )
在平面直角坐标系中,O为原点,点A(-3,0),点B(0,3),点E、点F分别为OA,OB的中点,若正方形OEDF绕点O顺时针旋转,得到正方形OE′D′F′,若直线AE′与直线BF′相交于点P,则点P的纵坐标的最大值是( )
 在平面直角坐标系中,O为原点,点A(-3,0),点B(0,3),点E、点F分别为OA,OB的中点,若正方形OEDF绕点O顺时针旋转,得到正方形OE′D′F′,若直线AE′与直线BF′相交于点P,则点P的纵坐标的最大值是( )
在平面直角坐标系中,O为原点,点A(-3,0),点B(0,3),点E、点F分别为OA,OB的中点,若正方形OEDF绕点O顺时针旋转,得到正方形OE′D′F′,若直线AE′与直线BF′相交于点P,则点P的纵坐标的最大值是( )| A. | $\frac{\sqrt{3}+1}{2}$ | B. | $\frac{\sqrt{3}+3}{2}$ | C. | $\frac{\sqrt{3}+3}{4}$ | D. | $\frac{3\sqrt{3}+3}{4}$ |
7.近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加.某商场从厂家购进了A、B两种型号的空气净化器,两种净化器的销售相关信息见下表:
(1)每台A型空气净化器和B型空气净化器的销售利润分别是多少?
(2)该公司计划一次购进两种型号的空气净化器共100台,其中B型空气净化器的进货量不少于A型空气净化器的2倍,为使该公司销售完这100台空气净化器后的总利润最大,请你设计相应的进货方案;
(3)已知A型空气净化器的净化能力为300m3/小时,B型空气净化器的净化能力为200m3/小时,某长方体室内活动场地的总面积为200m2,室内墙高3m,该场地负责人计划购买5台空气净化器每天花费30分钟将室内就欧诺个气净化一新,若不考虑空气对流等因素,至少要购买A型空气净化器多少台?
| A型销售数量(台) | B型销售数量(台) | 总利润(元) |
| 5 | 10 | 2000 |
| 10 | 5 | 2500 |
(2)该公司计划一次购进两种型号的空气净化器共100台,其中B型空气净化器的进货量不少于A型空气净化器的2倍,为使该公司销售完这100台空气净化器后的总利润最大,请你设计相应的进货方案;
(3)已知A型空气净化器的净化能力为300m3/小时,B型空气净化器的净化能力为200m3/小时,某长方体室内活动场地的总面积为200m2,室内墙高3m,该场地负责人计划购买5台空气净化器每天花费30分钟将室内就欧诺个气净化一新,若不考虑空气对流等因素,至少要购买A型空气净化器多少台?
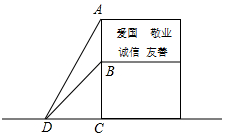 为了弘扬“社会主义核心价值观”,区政府在广场上竖立了如图所示的公益广告牌,并在两侧加固钢缆,已知钢缆底端D到达广告牌立柱AC的距离为5米,从点D测得广告牌顶端A点和底端B点的仰角分别为60°和45°,求广告牌的高度AB.
为了弘扬“社会主义核心价值观”,区政府在广场上竖立了如图所示的公益广告牌,并在两侧加固钢缆,已知钢缆底端D到达广告牌立柱AC的距离为5米,从点D测得广告牌顶端A点和底端B点的仰角分别为60°和45°,求广告牌的高度AB.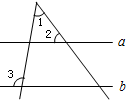 如图,直线a∥b,若∠1=55°,∠2=60°,则∠3=115°.
如图,直线a∥b,若∠1=55°,∠2=60°,则∠3=115°.