题目内容
3. 某区八年级有3000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:
某区八年级有3000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:| 成绩x(分) | 频数 | 频率 |
| 50≤x<60 | 10 | a |
| 60≤x<70 | 16 | 0.08 |
| 70≤x<80 | b | 0.20 |
(1)a=0.05,b=40.
(2)在扇形统计图中,“成绩x满足50≤x<60“对应扇形的圆心角度数是18°;
(3)若将得分转化为等级,规定:50≤x<60评为D,60≤x<70评为C,70≤x<90评为B,90≤x<100评为A.这次全区八年级参加竞赛的学生约有1530人参赛成绩被评为“B”.
分析 (1)根据题意可以求得a、b的值,从而可以将统计图补充完整;
(2)用360°乘以50≤x<60的频率可得;
(3)根据图中的数据可以求得这次全区八年级参加竞赛的学生约有多少学生参赛成绩被评为“B”.
解答 解:(1)本次调查的总人数为16÷0.08=200,
则a=10÷200=0.05,b=200×0.2=40,
故答案为:0.05,40;
(2)“成绩x满足50≤x<60“对应扇形的圆心角度数是360°×0.05=18°,
故答案为:18°;
(3)3000×$\frac{40+62}{200}$=1530,
即全区八年级参加竞赛的学生约有1530人参赛成绩被评为“B”,
故答案为:1530.
点评 本题考查频数分布直方图、频数分布表,解题的关键明确题意,利用数形结合的思想解答.

练习册系列答案
相关题目
13. 如图,分别以边长等于2的正方形的四边为直径作半圆,则圆中阴影部分的面积为( )
如图,分别以边长等于2的正方形的四边为直径作半圆,则圆中阴影部分的面积为( )
 如图,分别以边长等于2的正方形的四边为直径作半圆,则圆中阴影部分的面积为( )
如图,分别以边长等于2的正方形的四边为直径作半圆,则圆中阴影部分的面积为( )| A. | $\frac{π}{2}$-1 | B. | 2π-2 | C. | π+1 | D. | 2π-4 |
11. 如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
(1)求证:DF是⊙O的切线;
(2)若AC=3AE,写出求tanC的思路.
 如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.(1)求证:DF是⊙O的切线;
(2)若AC=3AE,写出求tanC的思路.
18.已知点A(a,2)与点B(3,b)关于x轴对称,则实数a,b的值是( )
| A. | a=3,b=2 | B. | a=-3,b=2 | C. | a=3,b=-2 | D. | a=-3,b=-2 |
8.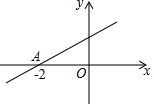 如图,直线y=kx+b与x轴的交点为A(-2,0),则不等式kx+b>0的解集为( )
如图,直线y=kx+b与x轴的交点为A(-2,0),则不等式kx+b>0的解集为( )
 如图,直线y=kx+b与x轴的交点为A(-2,0),则不等式kx+b>0的解集为( )
如图,直线y=kx+b与x轴的交点为A(-2,0),则不等式kx+b>0的解集为( )| A. | x>2 | B. | x≤2 | C. | x>-2 | D. | x≤-2 |
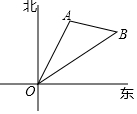 如图,海岛A在灯塔O处北偏东25°,海岛B在灯塔O处北偏东55°,海岛A在海岛B的北偏西80°,已知海岛A到灯塔的距离为80海里,求海岛B到灯塔的距离.(结果保留根号)
如图,海岛A在灯塔O处北偏东25°,海岛B在灯塔O处北偏东55°,海岛A在海岛B的北偏西80°,已知海岛A到灯塔的距离为80海里,求海岛B到灯塔的距离.(结果保留根号)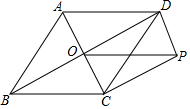 如图,在菱形ABCD中,AC、BD交于点O,BD=8,AC=4,DP∥AC,CP∥BD.
如图,在菱形ABCD中,AC、BD交于点O,BD=8,AC=4,DP∥AC,CP∥BD.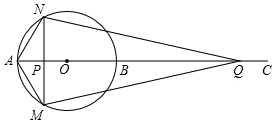 如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为$\frac{3}{2}$cm,AC=8cm,设运动时间为t秒.
如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为$\frac{3}{2}$cm,AC=8cm,设运动时间为t秒.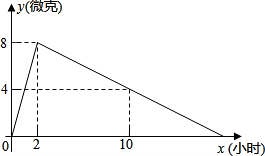 某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克(1微克=10-3毫克),接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克),随时间x(小时)的变化如图所示,当成人按规定剂量服药后,
某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克(1微克=10-3毫克),接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克),随时间x(小时)的变化如图所示,当成人按规定剂量服药后,