题目内容
18.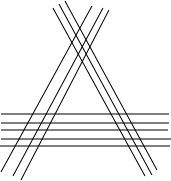 如图所示三组平行线分别有m,n,k条,在此图形中:
如图所示三组平行线分别有m,n,k条,在此图形中:(1)共有多少个三角形?
(2)共有多少个平行四边形?
分析 (1)当三组平行线各有一条时,有1个三角形,当三组平行线各有两条时,有2×2×2=8个三角形,当三组平行线各有三条时,有3×3×3=27个三角形,…当三组平行线分别有m,n,k条,三角形的个数为m•n•k;
(2)当三组各有两条,有3个平行四边形,当三组各有三条,有3×3+3×3+3×3个平行四边形,当三组各有四条,有6×6+6×6+6×6个平行四边形,…当三组平行线分别有m,n,k条,共有(1+2+3+…+m-1)(1+2+3+••+n-1)+(1+2+3+4+…k-1)(1+2+3+…+m-1)+(1+2+3+••+n-1)(1+2+3+4+…k-1)个平行四边形.
解答 解:(1)当三组平行线各有一条时,有1个三角形,
当三组平行线各有两条时,有2×2×2=8个三角形,
当三组平行线各有三条时,有3×3×3=27个三角形,
…
当三组平行线分别有m,n,k条,三角形的个数为m•n•k;
(2)当三组各有两条,有3个平行四边形,
当三组各有三条,有3×3+3×3+3×3个平行四边形,
当三组各有四条,有6×6+6×6+6×6个平行四边形,
…
当三组平行线分别有m,n,k条,
共有(1+2+3+…+m-1)(1+2+3+••+n-1)+(1+2+3+4+…k-1)(1+2+3+…+m-1)+(1+2+3+••+n-1)(1+2+3+4+…k-1)=$\frac{1}{4}$m(m-1)n(n-1)+$\frac{1}{4}$m(m-1)k(k-1)+$\frac{1}{4}$k(k-1)n(n-1)个平行四边形.
点评 此题考查图形的变化规律,找出图形之间的联系,从简单到复杂,找出规律解决问题.

练习册系列答案
相关题目
8. 如图,抛物线y1=x2+6x+10与y2=-x2+4x-6的顶点分别为A,B,点M(m,0)是x轴上的一个动点,则当MA+MB的值最小时,m的值是( )
如图,抛物线y1=x2+6x+10与y2=-x2+4x-6的顶点分别为A,B,点M(m,0)是x轴上的一个动点,则当MA+MB的值最小时,m的值是( )
 如图,抛物线y1=x2+6x+10与y2=-x2+4x-6的顶点分别为A,B,点M(m,0)是x轴上的一个动点,则当MA+MB的值最小时,m的值是( )
如图,抛物线y1=x2+6x+10与y2=-x2+4x-6的顶点分别为A,B,点M(m,0)是x轴上的一个动点,则当MA+MB的值最小时,m的值是( )| A. | -$\frac{3}{4}$ | B. | -$\frac{4}{3}$ | C. | -$\frac{4}{5}$ | D. | -$\frac{5}{4}$ |
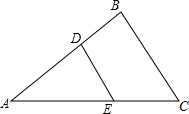 如图,在△ABC中,点D、E分别在AB和AC边上,若$\frac{AB}{AC}$=$\frac{AD}{AE}$=$\frac{4}{5}$,EC=4cm,求线段BD的长.
如图,在△ABC中,点D、E分别在AB和AC边上,若$\frac{AB}{AC}$=$\frac{AD}{AE}$=$\frac{4}{5}$,EC=4cm,求线段BD的长.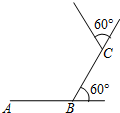 如图,小东在操场的中心位置,从点A出发,每走6m向左转60°,
如图,小东在操场的中心位置,从点A出发,每走6m向左转60°,