题目内容
11.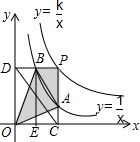 两个反比例函数y=$\frac{k}{x}$(k>1)和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P在y=$\frac{k}{x}$的图象上,PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,BE⊥x轴于点E,当点P在y=$\frac{k}{x}$的图象上运动时,以下结论:
两个反比例函数y=$\frac{k}{x}$(k>1)和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P在y=$\frac{k}{x}$的图象上,PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,BE⊥x轴于点E,当点P在y=$\frac{k}{x}$的图象上运动时,以下结论:①$\frac{PB}{PD}$=$\frac{PA}{PC}$;
②PA与PB始终相等;
③四边形PAOB的面积不会发生变化;
④△OBA的面积等于四边形ACEB的面积.
其中一定正确的是①③④(填写序号).
分析 设P(m,n),则mn=k,根据A、B两点在双曲线y=$\frac{1}{x}$上,且A点横坐标与P点横坐标相等,B点纵坐标与P点纵坐标相等,表示A、B两点的坐标,再对每个结论逐一判断.
解答 解:设P(m,n),则mn=k,
∵A、B两点在双曲线y=$\frac{1}{x}$上,
∴A(m,$\frac{1}{m}$),B($\frac{1}{n}$,n),
①∵$\frac{PB}{PD}$=$\frac{m-\frac{1}{n}}{m}$=$\frac{k-1}{k}$,$\frac{PA}{PC}$=$\frac{n}{n-\frac{1}{m}}$=$\frac{k-1}{k}$,∴$\frac{PB}{PD}$=$\frac{PA}{PC}$;结论①正确.
②∵PA=n-$\frac{1}{m}$=$\frac{k-1}{m}$,PB=m-$\frac{1}{n}$=$\frac{k-1}{n}$,PA≠PB,②结论错误;
③S四边形PAOB=S矩形OCPD-S△OBD-S△OAC=mn-$\frac{1}{2}$-$\frac{1}{2}$=k-1(定值),③结论正确;
④∴S△AOB=S四边形ABOC-S△AOC,
S四边形ABEC=S四边形ABOC-S△BOE,
∵S△AOC=S△BOE=$\frac{1}{2}$,
∴△OBA的面积等于四边形ACEB的面积,④结论正确;
故答案为:①③④,
点评 本题考查了反比例函数的综合题,关键是设P点坐标,利用点与点的坐标关系,反比例函数的性质表示相关线段的长,对每一个结论进行判断.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
13.下列说法正确的是( )
| A. | 了解飞行员视力的达标率应使用抽样调查 | |
| B. | 一组数据3,6,6,7,9的中位数是6 | |
| C. | 从2000名学生中选200名学生进行抽样调查,样本容量为2000 | |
| D. | 一组数据1,2,3,4,5的方差是10 |
2.将一个三角形改成与它相似的三角形,如果面积扩大为原来的9倍,那么周长扩大为原来的( )
| A. | 9倍 | B. | 3倍 | C. | 81倍 | D. | 18倍 |
1.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
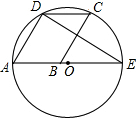 如图,已知平行四边形ABCD的顶点A、D、C在⊙O上,顶点B在⊙O的直径AE上,连接DE,若∠E=32°,则∠C=58°.
如图,已知平行四边形ABCD的顶点A、D、C在⊙O上,顶点B在⊙O的直径AE上,连接DE,若∠E=32°,则∠C=58°. 如图,抛物线l:y=-x2+bx+c(b,c为常数),其顶点E在正方形ABCD内或边上,已知点A(1,2),B(1,1),C(2,1).
如图,抛物线l:y=-x2+bx+c(b,c为常数),其顶点E在正方形ABCD内或边上,已知点A(1,2),B(1,1),C(2,1).
 某校对学生上学方式进行了一次抽样调查,并根据此次调查结果绘制了一个不完整的扇形统计图,其中“其他”部分所对应的圆心角是36°,则“步行”部分所占百分比是40%.
某校对学生上学方式进行了一次抽样调查,并根据此次调查结果绘制了一个不完整的扇形统计图,其中“其他”部分所对应的圆心角是36°,则“步行”部分所占百分比是40%.